Question

6．如圖．在平面直角坐標系中，△OBC的頂點O與坐標原點重合，點B的坐標為（-6，2$\sqrt{7}$），OC=15，BC=17，求線段OB的長度和△OBC的面積．

Answer 1

分析 在直角△OBM中利用勾股定理即可求得OB的長，然后根據勾股定理的逆定理證得△OBC是直角三角形，最后根據三角形面積公式即可求得三角形的面積．

解答 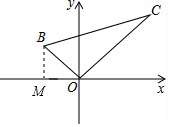解：過點B作BM⊥x軸于點M，
∵點B的坐標為（-6，2$\sqrt{7}$），
∴OM=6，BM=2$\sqrt{7}$，
由勾股定理得OB²=6²+（2$\sqrt{7}$）²=64，
∴OB=8．
∵8²+15²=17²，
∴OB²+OC²=BC²，
∴△OBC是直角三角形，且∠BOC=90°，
∴△OBC的面積=$\frac{1}{2}$×8×15=60．

點評 本題考查的是坐標和圖形的性質，勾股定理和逆定理，熟知性質定理是解答此題的關鍵．