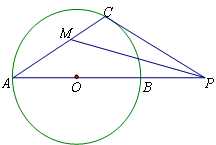
如圖8，⊙O的直徑AB=4，點P是AB延長線上的一點，過P點作⊙O 的切線，切點為C，連結(jié)AC.
（1）若∠CPA=30°，求PC的長；
（2）若點P在AB的延長線上運動，∠CPA的平分線交AC于點M. 你認為∠CMP的大小是否發(fā)生變化？若變化，請說明理由；若不變化，求出∠CMP的大小.
閱讀快車系列答案科目：初中數(shù)學 來源： 題型：
在平面直角坐標系中，已知拋物線y＝－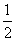
x2＋bx＋c (b，c為常數(shù))的頂點為P，等腰直角三角形ABC的頂點A的坐標為(0，–1)，C的坐標為(4，3)，直角頂點B在第四象限．
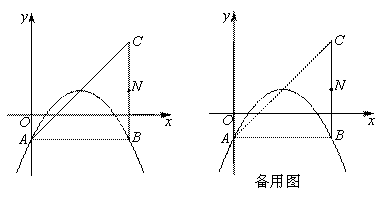
(1)如圖，若該拋物線過A，B兩點，求b，c的值；
(2)平移(1)中的拋物線，使頂點P在直線AC上滑動，且與直線AC交于另一點Q．
①點M在直線AC下方，且為平移前(1)中的拋物線上的點，當以M，P，Q三點為頂點的三角形是以PQ為腰的等腰直角三角形時，求點M的坐標；
②取BC的中點N，連接NP，BQ．當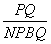
取最大值時，點Q的坐標為________.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
如圖3，是由矩形和半圓組成的一個封閉圖形，其中AB=8，AD=DE=FC=2，
點P由D點出發(fā)沿DE
半圓FC
運動，到達C點停止運動.設(shè)AP的長為x, △ABP的面積為y，
|
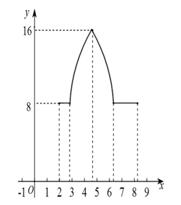
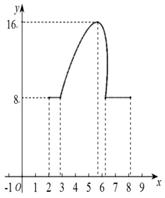
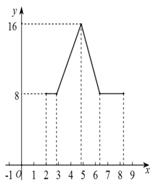
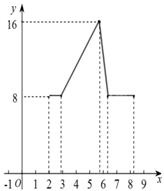
A B. C. D.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
概念：點P、Q分別是兩條線段a和b上任意一點，線段PQ長度的最小值叫做線段a與線段b的
“理想距離”．已知O（0，0），A（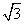
，1），B（m，n），C（m，n+2）是平面直角坐標系中四點．
（1） 根據(jù)上述概念，根據(jù)上述概念，完成下面的問題（直接寫答案）
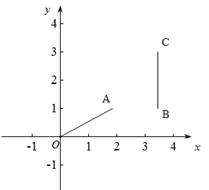
① 當m=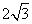
，n=1時，如圖13-1，線段BC與線段OA的理想距離是 2
；
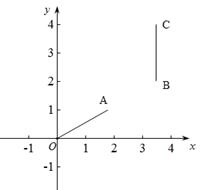
② 當m=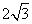，n=2時，如圖13-2，線段BC與線段OA的理想距離為 ；
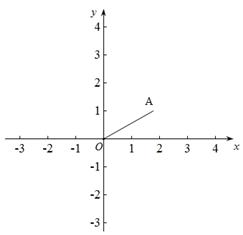
③ 當m=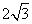，若線段BC與線段OA的理想距離為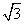,則n的取值范圍是 .
（2）如圖13-3，若點B落在圓心為A，半徑為1的圓上，
當n≥1時，線段BC與線段OA的理想距離記為d，則d的最小值為 (說明理由)
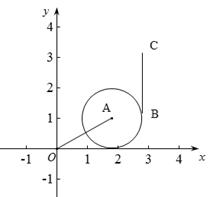（3）當m的值變化時，動線段BC與線段OA的距離始終為1，線段BC的中點為G，
求點G隨線段BC運動所走過的路徑長是多少？
|
|
|
|
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
在△ABC中，CA＝CB，在△AED中， DA＝DE，點D、E分別在CA、AB上，．
（1）如圖①，若∠ACB＝∠ADE＝90°，則CD與BE的數(shù)量關(guān)系是 ；
（2）若∠ACB＝∠ADE＝120°，將△AED繞點A旋轉(zhuǎn)至如圖②所示的位置，則CD與BE的數(shù)量關(guān)系是 ；，
（3）若∠ACB＝∠ADE＝2α（0°< α < 90°），將△AED繞點A旋轉(zhuǎn)至如圖③所示的位置，探究線段C
D與BE的數(shù)量關(guān)系，并加以證明(用含α的式子表示)．
 | |||||
 | |||||
 | |||||
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
為⊙O的切線，
的大小沒有變化
是AC上的一點，且AD=BC，DE
AC于D， ∠EAB=90º．
，求代數(shù)式
的值.
的整數(shù)解.