Question

17．如圖，直線y=-x+3與x軸，y軸分別相交于點B、點C，經(jīng)過B、C兩點的拋物線y=ax²+bx+c與x軸的另一交點為A，點A在點B的左邊，頂點為P，且線段AB的長為2．
（1）求點A的坐標(biāo)；
（2）求該拋物線的函數(shù)表達(dá)式；
（3）在拋物線的對稱軸上是否存在點G，使|GC-GB|最大？若存在，求G點坐標(biāo)；若不存在說明理由．
（3）連結(jié)AC，請問在x軸上是否存在點Q，使得以點P，B，Q為頂點的三角形與△ABC相似？若存在，請求出點Q的坐標(biāo)；若不存在，請說明理由．

Answer 1

分析 （1）求值直線y=-x+3與x軸的交點B，然后根據(jù)AB的長，即可求得OA的長，則A的坐標(biāo)即可求得；
（2）利用待定系數(shù)法求得二次函數(shù)的解析式；
（3）由于A、B兩點關(guān)于拋物線的對稱軸即直線x=2對稱，所以G點為直線CA與直線x=2的交點，先運用待定系數(shù)法求出直線AC的解析式，再令x=2，求出y的值，進而得出G點坐標(biāo)；
（4）分成$\frac{BQ}{BC}$=$\frac{PB}{AB}$，∠PBQ=∠ABC=45°和$\frac{QB}{AB}$=$\frac{PB}{BC}$，∠QBP=∠ABC=45°兩種情況求得QB的長，據(jù)此即可求解．

解答 解：（1）當(dāng)y=0時，-x+3=0，解得x=3，即B（3，0），
由AB=2，得3-2=1，
A的坐標(biāo)為（1，0）；
（2）根據(jù)題意得：$\left\{\begin{array}{l}{a+b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$，
則拋物線的解析式是：y=x²-4x+3；
（3）延長CA，交對稱軸于點G，連接GB，則|GC-GB|=GC-GA=AC最大．
∵拋物線y=x²-4x+3與x軸交于點A、點B（3，0），且對稱軸為直線x=2，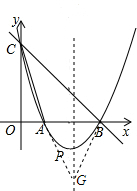
∴點A的坐標(biāo)為（1，0）．
設(shè)直線AC的解析式為y=kx+m，
∵A（1，0），C（0，3），
∴$\left\{\begin{array}{l}{k+m=0}\\{m=3}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=-3}\\{m=3}\end{array}\right.$，
∴y=-3x+3，
當(dāng)x=2時，y=-3×2+3=-3，
∴G點坐標(biāo)為（2，-3）；
（4）①當(dāng)$\frac{BQ}{BC}$=$\frac{PB}{AB}$，∠PBQ=∠ABC=45°時，△PBQ∽△ABC．
即$\frac{BQ}{3\sqrt{2}}$=$\frac{\sqrt{2}}{2}$
∴BQ=3，
又∵BO=3，
∴點Q與點O重合，
∴Q₁的坐標(biāo)是（0，0）．
②當(dāng)$\frac{QB}{AB}$=$\frac{PB}{BC}$，∠QBP=∠ABC=45°時，△QBP∽△ABC．
即$\frac{QB}{2}$=$\frac{\sqrt{2}}{3\sqrt{2}}$，
QB=$\frac{2}{3}$．
∵OB=3，
∴OQ=OB-QB=3-$\frac{2}{3}$=$\frac{7}{3}$
∴Q₂的坐標(biāo)是（$\frac{7}{3}$，0）．
∵∠PBx=180°-45°=135°，∠BAC＜135°，
∴∠PBx≠∠BAC．
∴點Q不可能在B點右側(cè)的x軸上
綜上所述，在x軸上存在兩點Q₁（0，0），Q₂（$\frac{7}{3}$，0）

點評 本題是二次函數(shù)的綜合題型，其中涉及到的知識點有運用待定系數(shù)法求二次函數(shù)的解析式，相似三角形的判定與性質(zhì)，正確進行分類求得QB的長是關(guān)鍵．