
【題目】某廠計劃一個月安裝新式兒童小機器人玩具480臺.由于熟練工不夠,工廠決定招聘一些新工人,新工人經過培訓后上崗.調研部門發現:1名熟練工和2名新工人每天可安裝16臺小機器人玩具;3名熟練工和4名新工人每天可安裝40臺小機器人玩具.
(1)每名熟練工和新工人每天分別可以安裝多少臺小機器人玩具?
(2)如果工廠招聘![]() 名新工人,使得招聘的新工人和抽調的熟練工剛好能完成一個月的安裝任務,那么工廠有哪幾種新工人的招聘方案?
名新工人,使得招聘的新工人和抽調的熟練工剛好能完成一個月的安裝任務,那么工廠有哪幾種新工人的招聘方案?
【答案】(1)每名熟練工和新工人每天分別可以安裝8、4臺小機器人玩具;(2)工廠有4種新工人的招聘方案:①招聘新工人8人,抽調熟練工4人;②招聘新工人6人,抽調熟練工5人;③招聘新工人4人,抽調熟練工6人;④招聘新工人2人,抽調熟練工7人.
【解析】
(1)設每名熟練工和新工人每天分別可以安裝x、y臺小機器人玩具,根據等量關系,列出關于x,y的二元一次方程組,即可求解;
(2)設工廠抽調a名熟練工,“招聘的新工人和抽調的熟練工剛好能完成一個月的安裝任務”,列出關于a,n的二元一次方程,進而即可得到結論.
(1)設每名熟練工和新工人每天分別可以安裝x、y臺小機器人玩具.
根據題意,得:![]() ,解得:
,解得:![]() .
.
答:每名熟練工和新工人每天分別可以安裝8、4臺小機器人玩具;
(2)設工廠抽調a名熟練工,
根據題意,得:30(8a+4n)=480, 2a+n=16,n=16-2a,
∵a,n都是正整數,0<n<10,
∴n=8,6,4,2.
即工廠有4種新工人的招聘方案:
①n=8,a=4,即招聘新工人8人,抽調熟練工4人;
②n =6,a=5,即招聘新工人6人,抽調熟練工5人;
③n =4,a=6,即招聘新工人4人,抽調熟練工6人;
④n =2,a=7,即招聘新工人2人,抽調熟練工7人.


科目:初中數學 來源: 題型:
【題目】從汽車燈的點O處發出的一束光線經燈的反光罩反射后沿CO方向平行射出,如入射光線OA的反射光線為AB,∠OAB=75°.在如圖中所示的截面內,若入射光線OD經反光罩反射后沿DE射出,且∠ODE=22°.則∠AOD的度數是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列說法錯誤的是( )
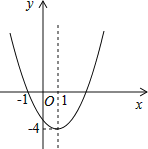
A.圖象關于直線x=1對稱
B.函數y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的兩個根
D.當x<1時,y隨x的增大而增大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某公園一圓形噴水池,水流在各個方向沿形狀相同的拋物線落下,建立如下圖所示的坐標系,如果噴頭所在處A(0,1.25),水流路線最高處M(1,2.25),則該拋物的解析式為__________________________。如果不考慮其他因素,那么水池的半徑至少要______m,才能使噴出的水流不至落到池外.
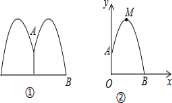
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:有一個直角三角形ABC,∠C=90°,AC=12,BC=5,一條線段PQ=AB,P、Q兩點分別在AC和過點A且垂直于AC的射線AX上運動,問P點運動到離A的距離等于___________時,ΔABC與以A、P、Q為頂點的三角形全等.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某倉庫調撥一批物資,調進物資共用8小時,調進物資4小時后同時開始調出物資(調進與調出的速度保持不變).該倉庫庫存物資W(噸)與時間t(小時)之間的函數關系如圖所示.則這批物資從開始調進到全部調出所需要的時間是( )

A. 8.4小時 B. 8.6小時 C. 8.8小時 D. 10小時
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com