

分析 (1)以直徑為斜邊,直角邊分別為2和6的圓內接直角三角形滿足要求;
(2)以直徑為斜邊,直角邊分別為2$\sqrt{2}$和4$\sqrt{2}$的圓內接直角三角形滿足要求;
(3)以直徑為斜邊,直角邊為2$\sqrt{5}$的圓內接等腰直角三角形滿足要求.
解答 解:(1)如圖1所示,△ABC即為所求三角形,其中AC=2,BC=6;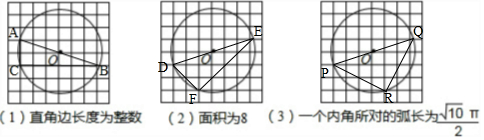
(2)如圖2所示,△DEF即為所求作三角形,其中DF=2$\sqrt{2}$,EF=4$\sqrt{2}$,
則其面積為$\frac{1}{2}$×2$\sqrt{2}$×4$\sqrt{2}$=8;
(3)如圖3所示,△PQR即為所求作三角形,其中PR=QR,∠PRQ=90°,
∵PQ=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
∴∠PRQ所對弧長為$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{10}}{2}$π.
點評 本題主要考查了圓周角定理的推論、勾股定理、弧長公式等知識點,理解新定義是解題的根本,熟練掌握直徑所對圓周角是直角是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源:2017屆吉林省九年級下學期第二次月考數學試卷(解析版) 題型:填空題
如圖,在△ABC中,DE∥BC,AD=6,BD=3,AE=4,則EC的長為_________.

查看答案和解析>>
科目:初中數學 來源:2017屆遼寧省丹東市九年級第一次模擬考試數學試卷(解析版) 題型:判斷題
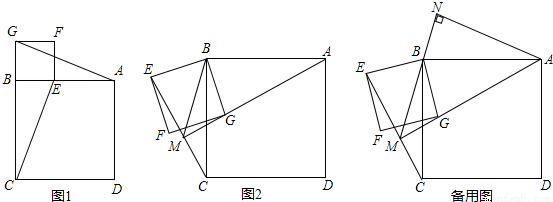
如圖,四邊形ABCD、BEFG均為正方形,
(1)如圖1,連接AG、CE,試判斷AG和CE的數量和位置關系并證明.
(2)將正方形BEFG繞點B順時針旋轉β角(0°<β<180°),如圖2,連接AG、CE相交于點M,連接MB,當角β發生變化時,∠EMB的度數是否發生變化?若不變化,求出∠EMB的度數;若發生變化,請說明理由.
(3)在(2)的條件下,過點A作AN⊥MB交MB的延長線于點N,請直接寫出線段CM與BN的數量關系.
查看答案和解析>>
科目:初中數學 來源:2017屆遼寧省丹東市九年級第一次模擬考試數學試卷(解析版) 題型:單選題
如圖,在△ABC中,AD和BE是高,∠ABE=45°,點F是AB的中點,AD與FE、BE分別交于點G、H,∠CBE=∠BAD.有下列結論:①FD=FE;②AH=2CD;③BC•AD= AE2;④∠DFE=2∠DAC ;⑤若連接CH,則CH∥EF.其中正確的個數為( )
AE2;④∠DFE=2∠DAC ;⑤若連接CH,則CH∥EF.其中正確的個數為( )
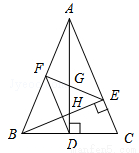
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
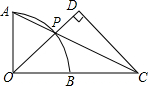 如圖,點O為弧AB所在圓的圓心,OA⊥OB,點P在弧AB上,AP的延長線與OB的延長線交于點C,過點C作CD⊥OP于D.若OB=BC=1,則PD的長為( )
如圖,點O為弧AB所在圓的圓心,OA⊥OB,點P在弧AB上,AP的延長線與OB的延長線交于點C,過點C作CD⊥OP于D.若OB=BC=1,則PD的長為( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com