
【題目】如圖,在直角坐標平面內有兩點![]() 、
、![]() ,且
,且![]() 、
、![]() 兩點之間的距離等于
兩點之間的距離等于![]() (
(![]() 為大于0的已知數),在不計算
為大于0的已知數),在不計算![]() 的數值條件下,完成下列兩題:
的數值條件下,完成下列兩題:
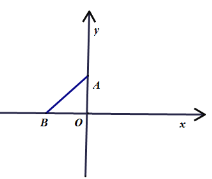
(1)以學過的知識用一句話說出![]() 的理由;
的理由;
(2)在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 是等腰三角形,如果存在,請寫出點
是等腰三角形,如果存在,請寫出點![]() 的坐標,并求
的坐標,并求![]() 的面積;如果不存在,請說明理由.
的面積;如果不存在,請說明理由.
【答案】(1)垂線段最短;(2)存在,當![]() ,
,![]() ;當
;當![]() ,
,![]() ;當
;當![]() ,
,![]() ;當
;當![]() ,
,![]() .
.
【解析】
(1)利用垂線段最短即可得出結論;
(2)分類討論,利用等腰三角形的判定可得出P點坐標,利用三角形面積公式得出結論.
解:(1)∵在平面直角坐標系中,AO⊥BO,O為垂足,
∴AO表示A點到直線BO的距離,
∵![]() ,
,
∴![]() ,
,
∵垂線段最短,且![]() 不與O重合,
不與O重合,
∴![]() ,即
,即![]() ,
,
∴![]() 的理由是“垂線段最短”;
的理由是“垂線段最短”;
(2)在![]() 軸上存在點
軸上存在點![]() ,使
,使![]() 是等腰三角形,
是等腰三角形,
①如圖1,當P在B點左邊,BP=BA=a,![]() 為等腰三角形,
為等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
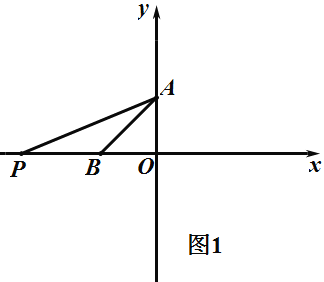
②如圖2,當P在B點右邊,BP=BA=a,![]() 為等腰三角形,
為等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
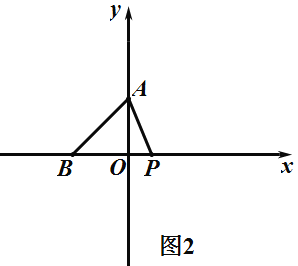
③如圖3,當P在B點右邊,BP=AP,![]() 為等腰三角形,
為等腰三角形,
此時P與O重合,即![]() ,
,
∵![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
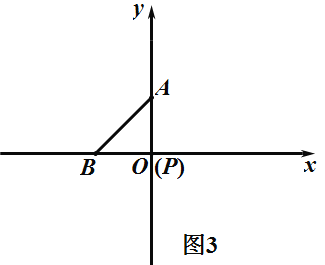
④如圖4,當P在B點右邊,AP=AB=a,![]() 為等腰三角形,
為等腰三角形,
∵AO⊥BO,
∴O為PB中點,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;

綜上所述:在![]() 軸上存在點
軸上存在點![]() ,使
,使![]() 是等腰三角形,
是等腰三角形,
當![]() ,
,![]() ;
;
當![]() ,
,![]() ;
;
當![]() ,
,![]() ;
;
當![]() ,
,![]() ;
;


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:
【題目】小聰和小明沿同一條筆直的馬路同時從學校出發到某圖書館查閱資料,學校與 圖書館的路程是 ![]() 千米,小聰騎自行車,小明步行,當小聰從原路回到學校時,小明剛好到 達圖書館,圖中折線
千米,小聰騎自行車,小明步行,當小聰從原路回到學校時,小明剛好到 達圖書館,圖中折線 ![]() 和線段
和線段 ![]() 分別表示兩人離學校的路程
分別表示兩人離學校的路程 ![]() (千米)與所經過的 時間
(千米)與所經過的 時間 ![]() (分鐘)之間的函數關系,請根據圖像回答下列問題:
(分鐘)之間的函數關系,請根據圖像回答下列問題:
(1)小聰在圖書館查閱資料的時間為 分鐘;小聰返回學校的速度為 千米/分鐘.
(2)請你求出小明離開學校的路程 ![]() (千米)與所經過的時間
(千米)與所經過的時間 ![]() (分鐘)之間的函數表達式;
(分鐘)之間的函數表達式;
(3)若設兩人在路上相距不超過 ![]() 千米時稱為可以“互相望見”,則小聰和小明可以“互相 望見”的時間共有多少分鐘?
千米時稱為可以“互相望見”,則小聰和小明可以“互相 望見”的時間共有多少分鐘?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直線ED經過點C,過A作AD⊥ED于點D,過B作BE⊥ED于點E.
求證:△BEC≌△CDA;
(模型應用)
(2)①已知直線l1:y=![]() x+4與坐標軸交于點A、B,將直線l1繞點A逆時針旋轉45o至直線l2,如圖2,求直線l2的函數表達式;
x+4與坐標軸交于點A、B,將直線l1繞點A逆時針旋轉45o至直線l2,如圖2,求直線l2的函數表達式;
②如圖3,長方形ABCO,O為坐標原點,點B的坐標為(8,-6),點A、C分別在坐標軸上,點P是線段BC上的動點,點D是直線y=-2x+6上的動點且在第四象限.若△APD是以點D為直角頂點的等腰直角三角形,請直接寫出點D的坐標.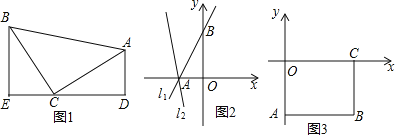
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,對稱軸為直線x= ![]() 的拋物線經過B(2,0)、C(0,4)兩點,拋物線與x軸的另一交點為A
的拋物線經過B(2,0)、C(0,4)兩點,拋物線與x軸的另一交點為A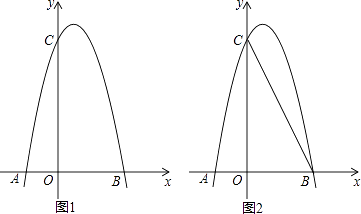
(1)求拋物線的解析式;
(2)若點P為第一象限內拋物線上的一點,設四邊形COBP的面積為S,求S的最大值;
(3)如圖2,若M是線段BC上一動點,在x軸是否存在這樣的點Q,使△MQC為等腰三角形且△MQB為直角三角形?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,解決提出的問題:
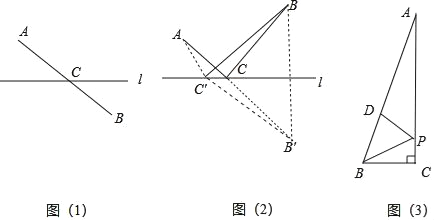
最短路徑問題:如圖(1),點A,B分別是直線l異側的兩個點,如何在直線l上找到一個點C,使得點C到點A,點B的距離和最短?我們只需連接AB,與直線l相交于一點,可知這個交點即為所求.
如圖(2),如果點A,B分別是直線l同側的兩個點,如何在l上找到一個點C,使得這個點到點A、點B的距離和最短?我們可以利用軸對稱的性質,作出點B關于的對稱點B,這時對于直線l上的任一點C,都保持CB=CB,從而把問題(2)變為問題(1).因此,線段AB與直線l的交點C的位置即為所求.
為了說明點C的位置即為所求,我們不妨在直線上另外任取一點C′,連接AC′,BC′,B′C′.因為AB′≤AC′+C′B′,∴AC+CB<AC'+C′B,即AC+BC最小.
任務:
數學思考
(1)材料中劃線部分的依據是 .
(2)材料中解決圖(2)所示問題體現的數學思想是 .(填字母代號即可)
A.轉化思想
B.分類討論思想
C.整體思想
遷移應用
(3)如圖,在Rt△ABC中,∠C=90°,∠BAC=15°,點P為C邊上的動點,點D為AB邊上的動點,若AB=8cm,則BP+DP的最小值為 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點A表示的數為8,B是數軸上一點,且AB=14.
![]()
(1)寫出數軸上點B表示的數;
(2)若點M、N分別是線段AO、BO的中點,求線段MN的長;
(3)若動點P從點A出發.以每秒5個單位長度的速度沿數軸向左勻速運動,動點Q從點B出發,以每秒3個單位長度的速度沿數軸向左勻速運動,若點P、Q同時出發.問點P運動多少秒時追上點Q?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李師傅負責修理我校課桌椅,現知道李師傅修理2張課桌和3把椅子共需86分鐘,修理5張課桌和2把椅子共需149分鐘.
(1)請問李師傅修理1張課桌和1把椅子各需多少分鐘
(2)現我校有12張課桌和14把椅子需要修理,要求1天做完,李師傅每天工作8小時,請問李師傅能在上班時間內修完嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上有A、B、C、D四個整數點![]() 即各點均表示整數
即各點均表示整數![]() ,且
,且![]() ,若A、D兩點表示的數的分別為
,若A、D兩點表示的數的分別為![]() 和6,點E為BD的中點,那么該數軸上上述五個點所表示的整數中,離線段BD的中點最近的整數是
和6,點E為BD的中點,那么該數軸上上述五個點所表示的整數中,離線段BD的中點最近的整數是![]()
![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖.AB是⊙O的直徑,E為弦AP上一點,過點E作EC⊥AB于點C,延長CE至點F,連接FP,使∠FPE=∠FEP,CF交⊙O于點D. 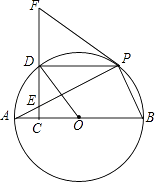
(1)證明:FP是⊙O的切線;
(2)若四邊形OBPD是菱形,證明:FD=ED.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com