Question

如圖，在等邊三角形ABC中，P是BC上的任意一點，線段AP的垂直平分線分別交AB、AC于點M、N．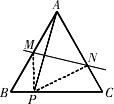

求證：BP·CP＝BM·CN．

Answer 1

答案：
解析：

分析：要證明BP·CP＝BM·CN，即證明＝．連接PM、PN，顯然線段BP與BM是△BPM的兩條邊，線段CN與CP是△CNP的兩條邊．所以，我們只需證明△BPM∽△CNP即可． 　　證明：連接PM、PN． 　　因為MN是AP的垂直平分線，所以MA＝MP，NA＝NP． 　　所以∠MPA＝∠MAP，∠NPA＝∠NAP． 　　所以∠MPN＝∠MPA＋∠NPA＝∠MAP＋∠NAP＝∠MAN＝60°． 　　所以∠BPM＋∠CPN＝180°－∠MPN＝120°． 　　因為∠BPM＋∠BMP＝180°－∠B＝120°，所以∠BMP＝∠CPN． 　　又因為∠B＝∠C＝60°，所以△BPM∽△CNP． 　　所以＝．所以BP·CP＝BM·CN． 　　點評：在題設的圖形中沒有明顯的三角形相似的情況下，我們可以順著要證明的比例線段中的字母，利用輔助線構造出三角形，再利用已知條件證明構造出來的三角形相似．