
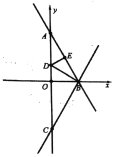
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 為線段
為線段![]() 的中點,
的中點,![]() 的平分線
的平分線![]() 與
與![]() 軸相較于點
軸相較于點![]() ,
,![]() 、
、![]() 兩點關于
兩點關于![]() 軸對稱.
軸對稱.
(1)一動點![]() 從點
從點![]() 出發,沿適當的路徑運動到直線
出發,沿適當的路徑運動到直線![]() 上的點
上的點![]() ,再沿適當的路徑運動到點
,再沿適當的路徑運動到點![]() 處.當
處.當![]() 的運動路徑最短時,求此時點
的運動路徑最短時,求此時點![]() 的坐標及點
的坐標及點![]() 所走最短路徑的長.
所走最短路徑的長.
(2)點![]() 沿直線
沿直線![]() 水平向右運動得點
水平向右運動得點![]() ,平面內是否存在點
,平面內是否存在點![]() 使得以
使得以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為菱形,若存在,請直接寫出點
為頂點的四邊形為菱形,若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)點![]() 的坐標為
的坐標為![]() ,點
,點![]() 所走最短路徑的長為
所走最短路徑的長為![]() ;(2)存在,點
;(2)存在,點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
【解析】
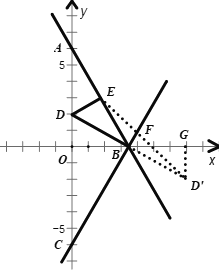
(1)先根據直線的解析式求出點A、B的坐標,再根據直角三角形和角平分線以及對稱的性質得出點C、D、E的坐標,然后利用待定系數法可求出直線BC的解析式,最后根據對稱性質確定最短路徑,求出直線![]() 的解析式,聯立兩個函數的解析式即可得;
的解析式,聯立兩個函數的解析式即可得;
(2)根據菱形的性質,分兩種情況:BD為邊和BD為對角線,然后分別利用菱形的性質、兩點之間的距離公式列出等式求解即可.
(1)對于![]()
當![]() 時,
時,![]() ,解得
,解得![]() ,則點B的坐標為
,則點B的坐標為![]()
當![]() 時,
時,![]() ,則點A的坐標為
,則點A的坐標為![]()
![]() 點
點![]() 為線段
為線段![]() 的中點
的中點
![]()
由點A、B的坐標得:![]()
在![]() 中,
中,![]() ,即
,即![]()
![]()
![]() 平分
平分![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
![]()
![]()
![]()
![]() 、
、![]() 兩點關于
兩點關于![]() 軸對稱
軸對稱
![]()
設直線BC的解析式為![]()
將點![]() 代入得
代入得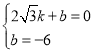 ,解得
,解得
則直線BC的解析式為![]()
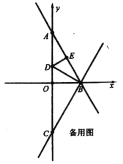
如圖,作點D關于直線BC的對稱點![]() ,連接ED交BC于點F
,連接ED交BC于點F
由對稱的性質、兩點之間線段最短可知,點P所走最短路徑的長為![]() 的長
的長
由對稱的性質可知,![]()
過點![]() 作
作![]() 軸于點G
軸于點G
在![]() 和
和![]() 中,
中,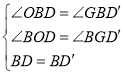
![]()
![]()
![]()
![]()
由兩點之間的距離公式得:![]()
設直線![]() 的解析式為
的解析式為![]()
將點![]() 代入得
代入得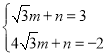 ,解得
,解得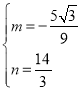
則直線![]() 的解析式為
的解析式為![]()
聯立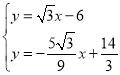 ,解得
,解得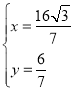
則點![]() 的坐標為
的坐標為![]() ;
;
(2)存在,點![]() 的坐標的求解過程如下:
的坐標的求解過程如下:
![]() ,點
,點![]() 沿直線
沿直線![]() 水平向右運動得點
水平向右運動得點![]()
![]() 可設點
可設點![]() 的坐標為
的坐標為![]() ,且
,且![]()
由菱形的性質,分以下兩種情況:
①若BD為邊
由菱形的定義得:![]()
由兩點之間的距離公式得:![]()
解得![]() 或
或![]() (舍去)
(舍去)
則點![]() 的坐標為
的坐標為![]()
②若BD為對角線
由菱形的定義得:![]()
由兩點之間的距離公式得:![]()
解得![]()
則點![]() 的坐標為
的坐標為![]()
綜上,點![]() 的坐標為
的坐標為![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,AB=10cm,E為對角線BD上一動點,連接AE,CE,過E點作EF⊥AE,交直線BC于點F.E點從B點出發,沿著BD方向以每秒2cm的速度運動,當點E與點D重合時,運動停止.設△BEF的面積為ycm2,E點的運動時間為x秒.
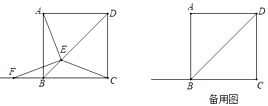
(1)求證:CE=EF;
(2)求y與x之間關系的函數表達式,并寫出自變量x的取值范圍;
(3)求△BEF面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數y=![]() +b(a、b為常數且a≠0)中,當x=2時,y=4;當x=﹣1時,y=1.請對該函數及其圖象進行如下探究:
+b(a、b為常數且a≠0)中,當x=2時,y=4;當x=﹣1時,y=1.請對該函數及其圖象進行如下探究:
(1)求該函數的解析式,并直接寫出該函數自變量x的取值范圍;
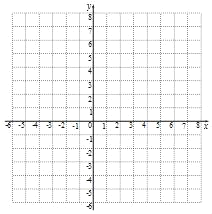
(2)請在下列直角坐標系中畫出該函數的圖象;
(3)請你在上方直角坐標系中畫出函數y=2x的圖象,結合上述函數的圖象,寫出不等式![]() +b≤2x的解集.
+b≤2x的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家所在居民樓的對面有一座大廈AB,高為74米,為測量居民樓與大廈之間的距離,小明從自己家的窗戶C處測得大廈頂部A的仰角為37°,大廈底部B的俯角為48°.
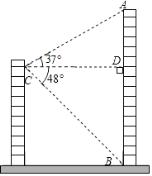
(1)求∠ACB的度數;
(2)求小明家所在居民樓與大廈之間的距離.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
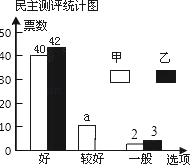
【題目】在校園歌手大賽中,甲、乙兩位同學的表現分外突出,現場A、B、C、D、E、F六位評委的打分情況以及隨機抽取的50名同學的民意調查結果分別如下統計表和不完整的條形統計圖:(說明:隨機抽取的50名同學每人必須從“好”、“較好”、“一般”中選一票投給每個選手)
A | B | C | D | E | F | |
甲 | 89 | 97 | 90 | 93 | 95 | 94 |
乙 | 89 | 92 | 90 | 97 | 94 | 94 |
(1)a= ,六位評委對乙同學所打分數的中位數是 ,并補全條形統計圖;
(2)學校規定評分標準如下:去掉評委評分中最高和最低分,再算平均分并將平均分與民意測評分按2:3計算最后得分.求甲、乙兩位同學的最后得分.(民意測評分=“好”票數×2+“較好”票數×1+“一般”票數×0)
查看答案和解析>>
科目:初中數學 來源: 題型:
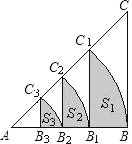
【題目】如圖,等腰Rt△ABC的直角邊長為4,以A為圓心,直角邊AB為半徑作弧BC1,交斜邊AC于點C1,C1B1⊥AB于點B1,設弧BC1,C1B1,B1B圍成的陰影部分的面積為S1,然后以A為圓心,AB1為半徑作弧B1C2,交斜邊AC于點C2,C2B2⊥AB于點B2,設弧B1C2,C2B2,B2B1圍成的陰影部分的面積為S2,按此規律繼續作下去,得到的陰影部分的面積S3=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x+6與反比例函數y=
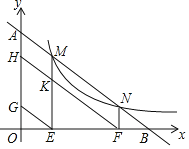
x+6與反比例函數y=![]() (k>0)的圖象交于點M、N,與x軸、y軸分別交于點B、A,作ME⊥x軸于點E,NF⊥x軸于點F,過點E、F分別作EG∥AB,FH∥AB,分別交y軸于點G、H,ME交HF于點K,若四邊形MKFN和四邊形HGEK的面積和為12,則k的值為_____.
(k>0)的圖象交于點M、N,與x軸、y軸分別交于點B、A,作ME⊥x軸于點E,NF⊥x軸于點F,過點E、F分別作EG∥AB,FH∥AB,分別交y軸于點G、H,ME交HF于點K,若四邊形MKFN和四邊形HGEK的面積和為12,則k的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
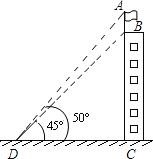
【題目】測量計算是日常生活中常見的問題,如圖,建筑物BC的屋頂有一根旗桿AB,從地面上D點處觀測旗桿頂點A的仰角為50°,觀測旗桿底部B點的仰角為45°,(可用的參考數據:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗桿的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D是BC邊的中點,連接AD,分別過點A,C作AE∥BC,CE∥AD交于點E,連接DE,交AC于點O.
(1)求證:四邊形ADCE是矩形;
(2)若AB=10,sin∠COE=![]() ,求CE的長.
,求CE的長.
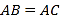
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com