
【題目】為獎勵在學校體育藝術節中表現突出的25名同學,派李老師為這些同學購買獎品,要求每人一件.李老師到文具店看了商品后,決定獎品在鋼筆和筆記本中選擇.如果買4個筆記本和2支鋼筆,則需86元;如果買3個筆記本和1支鋼筆,則需57元.
(1)求筆記本和鋼筆的單價分別為多少元?
(2)售貨員提示,購買筆記本沒有優惠;買鋼筆有優惠,具體方法是:如果買鋼筆超過10支,那么超出部分可以享受8折優惠,若買x(x>10)支鋼筆,所需總費用為y元,請你求出y與x之間的函數關系式;
(3)在(2)的條件下,如果買同一種獎品,請你幫忙計算說明,買哪種獎品費用更低.
【答案】(1)筆記本,鋼筆單價分別為14元,15元;(2)y=﹣2x+380;(3)買鋼筆費用低.
【解析】
(1)設筆記本的單價為x元,鋼筆的單價為y元,建立一個二元一次方程組求解即可得;
(2)先根據前10支鋼筆按原價、![]() 支鋼筆按8折優惠價購買,求出購買鋼筆所需費用,再根據學生人數和筆記本的價格求出購買筆記本的費用,兩者求和即可得;
支鋼筆按8折優惠價購買,求出購買鋼筆所需費用,再根據學生人數和筆記本的價格求出購買筆記本的費用,兩者求和即可得;
(3)分別計算出只購買筆記本和只購買鋼筆的費用,再比較大小即可得.
(1)設筆記本的單價為x元,鋼筆的單價為y元
由題意得![]()
解得![]()
答:設筆記本的單價為14元,鋼筆的單價為15元;
(2)由題意和(1)的結論得:購買鋼筆的費用為![]() (元);購買筆記本的費用為
(元);購買筆記本的費用為![]() (元)
(元)
則所需總費用為![]()
故y與x之間的函數關系式為![]() ;
;
(3)買25本筆記本費用為![]() (元)
(元)
買25支鋼筆費用:![]() (元)
(元)
![]()
![]() 購買鋼筆費用低
購買鋼筆費用低
答:如果買同一種獎品,則買鋼筆費用更低.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知關于![]() 的一元二次函數
的一元二次函數![]() (
(![]() )的圖象與
)的圖象與![]() 軸相交于
軸相交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,且
,且![]() ,頂點為
,頂點為![]() .
.
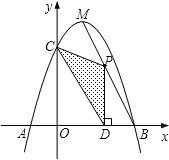
⑴ 求出一元二次函數的關系式;
⑵ 點![]() 為線段
為線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸的垂線
軸的垂線![]() ,垂足為
,垂足為![]() .若
.若![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并寫出
的函數關系式,并寫出![]() 的取值范圍;
的取值范圍;
⑶ 探索線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 為直角三角形,如果存在,求出
為直角三角形,如果存在,求出![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面上兩點A,B,給出如下定義:以點A或B為圓心,AB長為半徑的圓稱為點A,B的“確定圓”.如圖為點A,B的“確定圓”的示意圖.
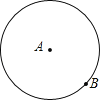
(1)已知點A的坐標為(-1,0),點B的坐標為(3,3),則點A,B的“確定圓”的面積為______;
(2)已知點A的坐標為(0,0),若直線y=x+b上只存在一個點B,使得點A,B的“確定圓”的面積為9π,求點B的坐標;
(3)已知點A在以P(m,0)為圓心,以1為半徑的圓上,點B在直線![]() 上,若要使所有點A,B的“確定圓”的面積都不小于9π,直接寫出m的取值范圍.
上,若要使所有點A,B的“確定圓”的面積都不小于9π,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與反比例函數
與反比例函數![]() 的圖象相交于
的圖象相交于![]() 、
、![]() 兩點,過
兩點,過![]() 、
、![]() 兩點分別作
兩點分別作![]() 軸的垂線,垂足分別為點
軸的垂線,垂足分別為點![]() 、
、![]() ,連接
,連接![]() 、
、![]() ,則四邊形
,則四邊形![]() 的面積為( )
的面積為( )
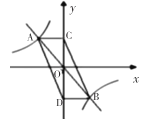
A.4B.8C.12D.24
查看答案和解析>>
科目:初中數學 來源: 題型:
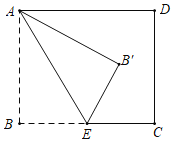
【題目】如圖,在矩形ABCD中,已知AB=2,點E是BC邊的中點,連接AE,△AB′E和△ABE關于AE所在直線對稱,若△B′CD是直角三角形,則BC邊的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2-2(k-3)x+k2-4k-1=0.
(1)若這個方程有實數根,求k的取值范圍;
(2)若這個方程有一個根為1,求k的值;
查看答案和解析>>
科目:初中數學 來源: 題型:
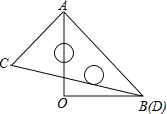
【題目】一副三角板按如圖所示疊放在一起,若固定△AOB,將△ACD繞著公共頂點A,按順時針方向旋轉α度(0°<α<180°),當△ACD的一邊與△AOB的某一邊平行時,相應的旋轉角α的值是___.
查看答案和解析>>
科目:初中數學 來源: 題型:
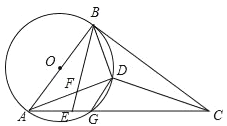
【題目】如圖:AB是⊙O的直徑,AC交⊙O于G,E是AG上一點,D為△BCE內心,BE交AD于F,且∠DBE=∠BAD.
(1)求證:BC是⊙O的切線;
(2)求證:DF=DG;
(3)若∠ADG=45°,DF=1,則有兩個結論:①ADBD的值不變;②AD-BD的值不變,其中有且只有一個結論正確,請選擇正確的結論,證明并求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知拋物線![]() 與x軸交于A(-1,0),B(3,0)兩點,與y軸交于點C.
與x軸交于A(-1,0),B(3,0)兩點,與y軸交于點C.
(1)求該拋物線的解析式;
(2)如圖①,若點D是拋物線上一動點,設點D的橫坐標為m(0<m<3),連接CD,BD,BC,AC,當△BCD的面積等于△AOC面積的2倍時,求m的值;
(3)若點N為拋物線對稱軸上一點,請在圖②中探究拋物線上是否存在點M,使得以B,C,M,N為頂點的四邊形是平行四邊形?若存在,請直接寫出所有滿足條件的點M的坐標;若不存在,請說明理由.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com