已知△ABC中,點(diǎn)G是△ABC的重心,過(guò)點(diǎn)G作DE∥BC,與AB相交于點(diǎn)D,與AC相交于點(diǎn)E,如果△ABC的面積為9.那么△ADE的面積是 .
【答案】
分析:根據(jù)DE∥BC判斷出△ADE和△ABC相似,再根據(jù)重心到頂點(diǎn)的距離等于到對(duì)邊中點(diǎn)的距離的2倍,求出兩三角形對(duì)應(yīng)中線(xiàn)的比,也就是相似比,再根據(jù)相似三角形面積的比等于相似比的平方列式計(jì)算即可得解.
解答: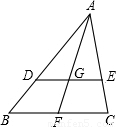
解:如圖所示,∵DE∥BC,
∴△ADE∽△ABC,
∵點(diǎn)G是△ABC的重心,
∴AG=2GF,
∴AG=

AF,
∴
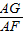
=

,
即△ADE和△ABC的相似比為

,
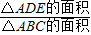
=(

)
2=

,
∵△ABC的面積為9,
∴△ADE的面積=

×9=4.
故答案為:4.
點(diǎn)評(píng):本題考查了三角形的重心,相似三角形的判定與性質(zhì),熟記三角形的重心到頂點(diǎn)的距離等于到對(duì)邊中點(diǎn)的距離的2倍求出兩三角形的對(duì)應(yīng)中線(xiàn)的比,也就是相似比是解題的關(guān)鍵.

 解:如圖所示,∵DE∥BC,
解:如圖所示,∵DE∥BC, AF,
AF,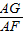 =
= ,
, ,
,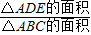 =(
=( )2=
)2= ,
, ×9=4.
×9=4.


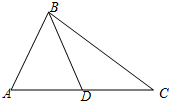 如圖,已知△ABC中,點(diǎn)D為邊AC的中點(diǎn),設(shè)
如圖,已知△ABC中,點(diǎn)D為邊AC的中點(diǎn),設(shè) 19、如圖,已知△ABC中,點(diǎn)F是BC的中點(diǎn),DE∥BC,則DG和GE有怎樣的關(guān)系?請(qǐng)你說(shuō)明理由.
19、如圖,已知△ABC中,點(diǎn)F是BC的中點(diǎn),DE∥BC,則DG和GE有怎樣的關(guān)系?請(qǐng)你說(shuō)明理由. 22、如圖,已知△ABC中,點(diǎn)D、E在BC上,AB=AC,AD=AE.請(qǐng)說(shuō)明BD=CE的理由.
22、如圖,已知△ABC中,點(diǎn)D、E在BC上,AB=AC,AD=AE.請(qǐng)說(shuō)明BD=CE的理由.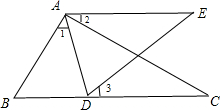 如圖所示,已知△ABC中,點(diǎn)D為BC邊上一點(diǎn),∠1=∠2=∠3,AC=AE,
如圖所示,已知△ABC中,點(diǎn)D為BC邊上一點(diǎn),∠1=∠2=∠3,AC=AE,