【題目】如圖，
、
是
的兩條半徑，
，點
在上，
與交于點
，點
在的延長線上，且
.
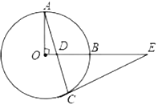
（1）求證：
是的切線;
（2）當
，
時，直接寫出
的長.
【答案】（1）見解析；（2）CD=
.
【解析】
（1）連接OC，利用等邊對等角和直角三角形的兩銳角互余證得OC⊥CE即可得出結論；
（2）在Rt△AOD中求得∠ADO=90°，進而得出∠EDC=90°，根據等邊三角形的判定可得△ECD是等邊三角形，得出∠E=60°，然后在Rt△OCE中利用三角函數求出CE的長，即可得出CD的長．
（1）證明：連接OC.
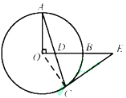
∵OA=OC,
∴∠A=∠OCD.
∵OA⊥OB,
∴∠AOB=90°.
∴∠A+∠ADO=90°.
∵CE=DE,
∴∠EDC=∠ECD=∠ADO.
∴∠OCD+∠ECD=90°.
∴OC⊥CE.
∵點C在⊙O上,
∴CE是⊙O的切線.
（2）解：∵OA⊥OB，
∴∠AOB=90°，
∴∠ADO=90°-∠A=90°-30°=60°，
∴∠EDC=∠ADO=60°，
∵CE=DE，
∴△ECD是等邊三角形，
∴CD=CE，∠E=60°．
在Rt△OCE中，
CE=
=
=．
∴CD=CE=．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
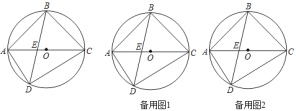
【題目】如圖，四邊形ABCD內接于⊙O．AC為直徑，AC、BD交于E，
=
．
（1）求證：AD+CD=
BD；
（2）過B作AD的平行線，交AC于F，求證：EA2+CF2=EF2；
（3）在（2）條件下過E，F分別作AB、BC的垂線垂足分別為G、H，連GH、BO交于M，若AG=3，S四邊形AGMO：S四邊形CHMO=8：9，求⊙O半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，拋物線
與直線
分別交于
軸、
軸上的
兩點，設該拋物線與軸的另一個交點為點
，頂點為點
，聯結
交軸于點
.
求該拋物線的表達式及點的坐標；
求
的正切值；
如果點
在軸上，且
，求點的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某水果批發商場經銷一種高檔水果，如果每千克盈利10元，每天可售出500千克．經市場調查發現，在進貨價不變的情況下，若每千克漲價1元，日銷售量將減少20千克．
（1）現該商場要保證每天盈利6 000元，同時又要顧客得到實惠，那么每千克應漲價多少元？
（2）若該商場單純從經濟角度看，每千克這種水果漲價多少元，能使商場獲利最多？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有兩個函數
和
，若對于每個使函數有意義的實數
，函數
的值為兩個函數值中中較小的數，則稱函數為這兩個函數、的較小值函數。例如：
，
，則、的較小值函數
（1）函數是函數
，
的較小值函數;
①在如圖的平面直角坐標系中畫出函數的圖像.
②寫出函數的兩條性質.
（2）函數是函數
，
的較小值函數，當
時，函數值的取值范圍為
.當
取某個范圍內的任意值時，
為定值.直接寫出滿足條件的的取值范圍及其對應的值.
（3）函數是函數
，
（
為常數，且
）的較小值函數，當
時，隨著的增大，函數值先增大后減小，直接寫出的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
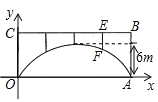
【題目】如圖，一座拱橋的輪廓是拋物線型，拱高6
，在長度為8的兩支柱
和
之間，還安裝著三根支柱，相鄰兩支柱間的距離為5.
（1）建立如圖所示的直角坐標系，求拱橋拋物線的函數表達式；
（2）求支柱
的長度.
（3）拱橋下面擬鋪設行車道，要保證高3的汽車能夠通過（車頂與拱橋的距離不小于0.3），行車道最寬可以鋪設多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平行四邊形ABCD放置在平面直角坐標系xOy中，已知A（-2，0），B（2，0），D（0，3），反比例函數y＝
（x＞0）的圖象經過點C．
（1）求此反比例函數的解析式；
（2）問將平行四邊形ABCD向上平移多少個單位，能使點B落在雙曲線上？
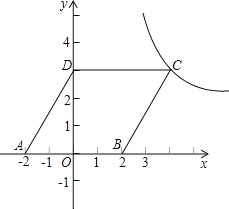
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
