如圖，四邊形ABCD、DEFG都是正方形，連接AE、CG,AE與CG相交于點M，CG與AD相交于點N。求證: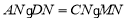
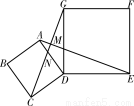
見解析
【解析】
試題分析：首先根據正方形的性質得到AD=CD，DE=DG，∠ADC=∠EDG，從而可以得到∠ADE=∠CDG，可以得到△ADE≌△CDG，根據全等得到∠DAE=∠DCG，再加上對頂角∠ANM=∠CND得到△AMN∽△CDN，從而說明所要證明的結論.
試題解析：∵四邊形ABCD和四邊形DEFG都是正方形，∴AD=CD，DE=DG，∠ADC=∠EDG=90°，
∵∠ADE=90°+∠ADG，∠CDG=90°+∠ADG，∴∠ADE=∠CDG， ∴△ADE≌△CDG（SAS），
∴∠DAE=∠DCG， 又∵∠ANM=∠CND， ∴△AMN∽△CDN， ∴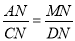
，
即AN•DN = CN•MN．
考點：
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源：2014-2015學年湖北省容城鎮三閭學校九年級上學期期中考試數學試卷（解析版） 題型：填空題
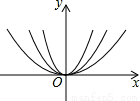
如圖所示,在同一坐標系中,作出①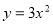
②
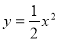③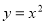
的圖象,則圖象從里到外的三條拋物線對應的函數依次是（填序號） 。
查看答案和解析>>
科目：初中數學 來源：2014-2015學年北京市燕山區九年級上學期期末考試數學試卷（解析版） 題型：填空題
在平面直角坐標系xOy中，對于任意三點A，B，C，給出如下定義：
若矩形的任何一條邊均與某條坐標軸平行，且A，B，C三點都在矩形的內部或邊界上，則稱該矩形為點A，B，C的外延矩形．點A，B，C的所有外延矩形中，面積最小的矩形稱為點A，B，C的最佳外延矩形．例如，圖中的矩形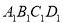
，
，
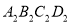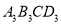都是點A，B，C的外延矩形，矩形
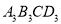是點A，B，C的最佳外延矩形．
（1）如圖1，已知A（－2，0），B（4，3），C（0，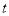
）．
①若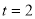
，則點A，B，C的最佳外延矩形的面積為 ；
②若點A，B，C的最佳外延矩形的面積為24，則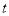的值為 ；
（2）如圖2，已知點M（6，0），N（0，8）．P（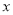
，
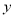）是拋物線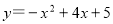
上一點，求點M，N，P的最佳外延矩形面積的最小值，以及此時點P的橫坐標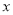的取值范圍；
（3）如圖3，已知點D（1，1）．E（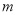
，
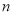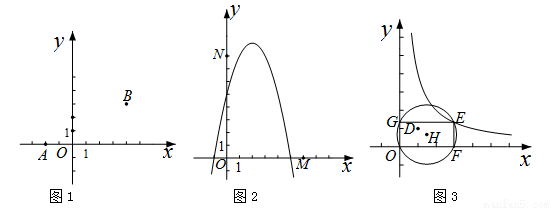
）是函數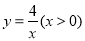
的圖象上一點，矩形OFEG是點O，D，E的一個面積最小的最佳外延矩形，⊙H是矩形OFEG的外接圓，請直接寫出⊙H的半徑r的取值范圍．
查看答案和解析>>
科目：初中數學 來源：2014-2015學年北京市燕山區九年級上學期期末考試數學試卷（解析版） 題型：選擇題
如圖，在Rt△OAB中，∠AOB＝90°，OA＝4，OB＝3．⊙O的半徑為2，點P是線段AB上的一動點，過點P作⊙O的一條切線PQ，Q為切點．設AP＝
，PQ2＝
，則與的函數圖象大致是
查看答案和解析>>
科目：初中數學 來源：2014-2015學年北京市通州區九年級上學期期末考試數學試卷（解析版） 題型：填空題
已知反比例函數圖象經過點（－1，3），那么這個反比例函數的表達式為_______________.
查看答案和解析>>
科目：初中數學 來源：2014-2015學年北京市通州區九年級上學期期末考試數學試卷（解析版） 題型：選擇題
如圖，為了測樓房BC的高，在距離樓房10米的A處，測得樓頂B的仰角為α，那么樓房BC的高為（ ）
A．10tanα（米） B．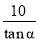
（米） C．10sinα（米） D．
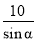（米）
查看答案和解析>>
科目：初中數學 來源：2014-2015學年北京市海淀區九年級上學期期末考試數學試卷（解析版） 題型：解答題
在平面直角坐標系
中，反比例函數
的圖象經過點
，
．
（1）求代數式mn的值；
（2）若二次函數
的圖象經過點B，求代數式
的值；
（3）若反比例函數
的圖象與二次函數
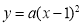的圖象只有一個交點，且該交點在直線
的下方，結合函數圖象，求
的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，求代數式
的值．