
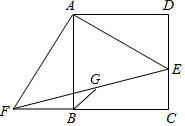
 E為正方形ABCD的邊CD上一點,將△ADE繞A點順時針旋轉90°,得△ABF,G為EF中點.下列結論:①G在△ABF的外接圓上;②EC=$\sqrt{2}$BG;③B,G,D三點在同一條直線上;④若S四邊形BGEC=$\frac{1}{4}$S正方形ABCD,那么E為DC的黃金分割點.正確的是( )
E為正方形ABCD的邊CD上一點,將△ADE繞A點順時針旋轉90°,得△ABF,G為EF中點.下列結論:①G在△ABF的外接圓上;②EC=$\sqrt{2}$BG;③B,G,D三點在同一條直線上;④若S四邊形BGEC=$\frac{1}{4}$S正方形ABCD,那么E為DC的黃金分割點.正確的是( )| A. | ①② | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
分析 先判斷出點A,F,B,G四點共圓即可得出①正確,再用線段的垂直平分線的判定即可得出③正確,進而判斷出∠CBD=45°,再判斷出GH是△CEF的中位線,判斷出,進而用等腰直角三角形的性質得出BG=$\sqrt{2}$BH即可得出②正確,利用S四邊形BGEC=$\frac{1}{4}$S正方形ABCD,判斷出CE=2DE,即可判斷出④錯誤.
解答 解: ∵將△ADE繞A點順時針旋轉90°,得△ABF,
∵將△ADE繞A點順時針旋轉90°,得△ABF,
∴∠EAF=90°,
∵G為EF中點.
∴EG=FG,∠AGF=90°,
∵四邊形ABCD是正方形,
∴AB=BC=CD=AD,∠ABF=∠ABC=∠ADC=∠BCD=90°,
∴∠AGF=∠ABF=90°,
∴點A,F,B,G四點共圓,
∴點G在△ABF的外接圓上;
所以①正確,
連接AC,在Rt△AEF中,EG=FG,
∴AG=$\frac{1}{2}$EF,
在Rt△CEF中,EG=FG,
∴CG=$\frac{1}{2}$EF,
∴AG=CG,
∴點G是線段AC的垂直平分線上,
∵AB=CB,
∴點B是線段AC的垂直平分線上,
∵AD=CD,
∴點D是線段AC的垂直平分線上,
∴點B,G,D都在線段AC的垂直平分線上,
∴B,G,D三點在同一條直線上;所以③正確,
∵B,G,D三點在同一條直線上;
∴∠CBD=∠ABD=$\frac{1}{2}$∠ABC=45°,
過點G作GH⊥BC,
∴GH∥CE,
∵EG=FG,
∴GH是△CEF的中位線,
∴CE=2GH,
在Rt△BHG中,∠CBD=45°,
∴BG=$\sqrt{2}$GH,
∴GH=$\frac{\sqrt{2}}{2}$BG,
∴CE=2×$\frac{\sqrt{2}}{2}$BG=$\sqrt{2}$BG,
所以②正確;
∵S四邊形BGEC=S△BHG+S梯形CEGH
=$\frac{1}{2}$GH2+$\frac{1}{2}$(GH+CE)×CH
=$\frac{1}{2}$GH2+$\frac{1}{2}$(GH+CE)×(BC-GH)
=$\frac{1}{2}$($\frac{1}{2}$CE)2+$\frac{1}{2}$($\frac{1}{2}$CE+CE)×(BC-$\frac{1}{2}$CE)
=$\frac{1}{8}$CE2+$\frac{3}{4}$CE×(BC-$\frac{1}{2}$CE)
=$\frac{3}{4}$CE×CD-$\frac{1}{4}$CD2,
S正方形ABCD=CD2,
∵S四邊形BGEC=$\frac{1}{4}$S正方形ABCD,
∴$\frac{3}{4}$CE×CD-$\frac{1}{4}$CD2=$\frac{1}{4}$CD2,
∴3CE=2CD=2(CE+DE),
∴CE=2DE,
∴E不是DC的黃金分割點.
所以④錯誤,
即:正確的有①②③,
故選B.
點評 此題是旋轉的性質,主要考查了正方形的性質,四點共圓,直角三角形的斜邊的直線等于斜邊的一半,等腰直角三角形的性質,幾何圖形的面積,三角形的中位線.判斷出B,G,D三點共線是解本題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,∠ACB=90°,AC=8,BC=6,P是直線AB上的動點(不與點B重合),將△BCP沿CP所在的直線翻折,得到△B′CP,連接B′A,B′A長度的最小值是m,B′A長度的最大值是n,則m+n的值等于16.
如圖,在△ABC中,∠ACB=90°,AC=8,BC=6,P是直線AB上的動點(不與點B重合),將△BCP沿CP所在的直線翻折,得到△B′CP,連接B′A,B′A長度的最小值是m,B′A長度的最大值是n,則m+n的值等于16.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC內接于⊙O,且AB為⊙O的直徑,∠ACB的平分線交⊙O于點D,過點D作⊙O的切線PD交CA的延長線于點P.
如圖,△ABC內接于⊙O,且AB為⊙O的直徑,∠ACB的平分線交⊙O于點D,過點D作⊙O的切線PD交CA的延長線于點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,∠C=90°,∠ABC=60°,若CD=2,AB=6,則S△ABD=$\frac{9\sqrt{3}}{2}$-3.
如圖,在△ABC中,∠C=90°,∠ABC=60°,若CD=2,AB=6,則S△ABD=$\frac{9\sqrt{3}}{2}$-3.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,三角形紙片ABC中,∠BCA=90°,在AC上取一點E,以BE為折痕進行翻折,使AB的一部分與BC重合,A與BC延長線上的點D重合,若∠A=30°,AC=6,則,DE的長度為( )
如圖,三角形紙片ABC中,∠BCA=90°,在AC上取一點E,以BE為折痕進行翻折,使AB的一部分與BC重合,A與BC延長線上的點D重合,若∠A=30°,AC=6,則,DE的長度為( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com