
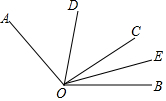
 如圖,∠AOB=130°,OC是∠AOB內部一條射線,OD平分∠AOC,OE平分∠BOC.求∠DOE的度數.
如圖,∠AOB=130°,OC是∠AOB內部一條射線,OD平分∠AOC,OE平分∠BOC.求∠DOE的度數. 分析 先根據角平分線定義得到∠EOC=$\frac{1}{2}$∠BOC,∠COD=$\frac{1}{2}$∠AOC,再求出∠EOD=∠EOC+∠COD=$\frac{1}{2}$∠AOB=65°.
解答 解:∵OD平分∠AOC (已知)
∴∠DOC=$\frac{1}{2}$∠AOC (角平分線定義)
∵OE平分∠BOC (已知)
∴∠COE=$\frac{1}{2}$∠COB (角平分線定義)
∵∠DOE=∠DOC+∠COE (如圖)
∴∠DOE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠COB
=$\frac{1}{2}$∠AOB (等式性質)
∵∠AOB=130° (已知)
∴∠DOE=$\frac{1}{2}$×130°
=65°.
點評 本題考查了角平分線定義和角的有關計算的應用,主要考查學生計算能力和推理能力,比較簡單.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 在小孔成像問題中,如圖所示,若為O到AB的距離是18cm,O到CD的距離是6cm,則像CD的長是物體AB長的( )
在小孔成像問題中,如圖所示,若為O到AB的距離是18cm,O到CD的距離是6cm,則像CD的長是物體AB長的( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2倍 | D. | 3倍 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com