
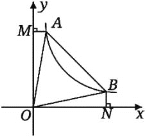
【題目】如圖,直線![]() 與雙曲線
與雙曲線![]() 交于A、B兩點,連接OA、OB,
交于A、B兩點,連接OA、OB,![]() 軸于點M,
軸于點M,![]() 軸于點N,有以下結論:①
軸于點N,有以下結論:①![]() ;②
;②![]() ;③
;③![]() 則
則![]() ;④當
;④當![]() 時,
時,![]() .其中結論正確的是___________
.其中結論正確的是___________
【答案】①②③④
【解析】
①②設A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),聯(lián)立y=-x+b與y=
),聯(lián)立y=-x+b與y=![]() 得
得![]() ,則
,則![]()
![]() =k,又
=k,又![]()
![]() =k,比較可知
=k,比較可知![]() =
=![]() ,同理可得
,同理可得![]() =
=![]() ,即ON=OM,AM=BN,可證結論;
,即ON=OM,AM=BN,可證結論;
③作OH⊥AB,垂足為H,根據(jù)對稱性可證△OAM≌△OAH≌△OBH≌△OBN,可證S△AOB=k;
④延長MA,NB交于G點,可證△ABG為等腰直角三角形,當AB=![]() 時,GA=GB=1,則ON-BN=GN-BN=GB=1;
時,GA=GB=1,則ON-BN=GN-BN=GB=1;
設A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),代入y=
),代入y=![]() 中,得
中,得![]()
![]() =
=![]()
![]() =k,
=k,
聯(lián)立 ,
,
得![]() ,
,
則![]()
![]() =k,又
=k,又![]()
![]() =k,
=k,
∴![]() =
=![]() ,
,
同理![]()
![]() =k,
=k,
可得![]() =
=![]() ,
,
∴ON=OM,AM=BN,
∵∠AMO=∠BNO=90![]() ,
,
∴△AOM≌△BON,②正確;
∴OA=OB,①正確;
③作OH⊥AB,垂足為H,
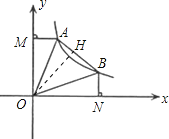
∵OA=OB,∠AOB=45°,且△AOM≌△BON,
∴∠MOA=∠BON=22.5°,∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=![]() ,正確;
,正確;
④延長MA,NB交于G點,
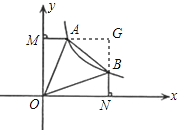
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG為等腰直角三角形,
當AB![]() 時,GA=GB=1,
時,GA=GB=1,
∴ON-BN=GN-BN=GB=1,正確;
綜上,①②③④都正確.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,正方形ABCD的頂點A,B在x軸的負半軸上,反比例函數(shù)y=![]() (k1≠0)在第二象限內(nèi)的圖象經(jīng)過正方形ABCD的頂點D(m,2)和BC邊上的點G(n,
(k1≠0)在第二象限內(nèi)的圖象經(jīng)過正方形ABCD的頂點D(m,2)和BC邊上的點G(n,![]() ),直線y=k2x+b(k2≠0)經(jīng)過點D,點G,則不等式
),直線y=k2x+b(k2≠0)經(jīng)過點D,點G,則不等式![]() ≤k2x+b的解集為__________.
≤k2x+b的解集為__________.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
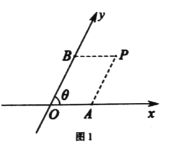
【題目】閱讀材料并解答下列問題:如圖1,把平面內(nèi)一條數(shù)軸![]() 繞原點
繞原點![]() 逆時針旋轉角
逆時針旋轉角![]() 得到另一條數(shù)軸
得到另一條數(shù)軸![]() 軸和
軸和![]() 軸構成一個平面斜坐標系
軸構成一個平面斜坐標系![]()
規(guī)定:過點![]() 作
作![]() 軸的平行線,交
軸的平行線,交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 軸的平行線,交
軸的平行線,交![]() 軸于點
軸于點![]() ,若點
,若點![]() 在
在![]() 軸對應的實數(shù)為
軸對應的實數(shù)為![]() ,點
,點![]() 在
在![]() 軸對應的實數(shù)為
軸對應的實數(shù)為![]() ,則稱有序實數(shù)對
,則稱有序實數(shù)對![]() 為點
為點![]() 在平面斜坐標系
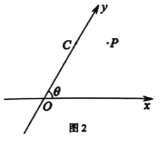
在平面斜坐標系![]() 中的斜坐標.如圖2,在平面斜坐標系
中的斜坐標.如圖2,在平面斜坐標系![]() 中,已知
中,已知![]() ,點
,點![]() 的斜坐標是
的斜坐標是![]() ,點
,點![]() 的斜坐標是
的斜坐標是![]()
(1)連接![]() ,求線段
,求線段![]() 的長;
的長;
(2)將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 到
到![]() (點
(點![]() 與點
與點![]() 對應),求點
對應),求點![]() 的斜坐標;
的斜坐標;
(3)若點![]() 是直線
是直線![]() 上一動點,在斜坐標系
上一動點,在斜坐標系![]() 確定的平面內(nèi)以點
確定的平面內(nèi)以點![]() 為圓心,
為圓心,![]() 長為半徑作
長為半徑作![]() ,當⊙
,當⊙![]() 與
與![]() 軸相切時,求點
軸相切時,求點![]() 的斜坐標,
的斜坐標,
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
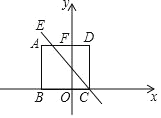
【題目】如圖所示, 在平面直角坐標系中, 邊長為![]() 的正方形
的正方形![]() 的邊
的邊![]() 在
在![]() 軸上,
軸上, ![]() 交
交![]() 軸于點
軸于點![]() ,一次函數(shù)
,一次函數(shù)![]() 的圖像經(jīng)過點
的圖像經(jīng)過點![]() ,且與線段
,且與線段![]() 始終有交點(含端點),若
始終有交點(含端點),若![]() ,則
,則![]() 的值可能為( )
的值可能為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
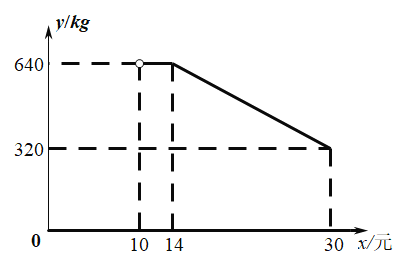
【題目】![]() 年春節(jié)期間,新型冠狀病毒肆虐,突如其來的疫情讓大多數(shù)人不能外出,網(wǎng)絡銷售成為這個時期最重要的一種銷售方式。某鄉(xiāng)鎮(zhèn)貿(mào)易公司因此開設了一家網(wǎng)店,銷售當?shù)啬撤N農(nóng)產(chǎn)品。已知該農(nóng)產(chǎn)品成本為每千克
年春節(jié)期間,新型冠狀病毒肆虐,突如其來的疫情讓大多數(shù)人不能外出,網(wǎng)絡銷售成為這個時期最重要的一種銷售方式。某鄉(xiāng)鎮(zhèn)貿(mào)易公司因此開設了一家網(wǎng)店,銷售當?shù)啬撤N農(nóng)產(chǎn)品。已知該農(nóng)產(chǎn)品成本為每千克![]() 元,調(diào)查發(fā)現(xiàn),每天銷售量
元,調(diào)查發(fā)現(xiàn),每天銷售量![]() 與銷售單價
與銷售單價![]() (元)滿足如圖所示的函數(shù)關系(其中
(元)滿足如圖所示的函數(shù)關系(其中![]() )
)
(1)求![]() 與
與![]() 之間的函數(shù)關系式并標出自變最
之間的函數(shù)關系式并標出自變最![]() 的取值范圍;
的取值范圍;
(2)當銷售單價x為多少元時,每天的銷售利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
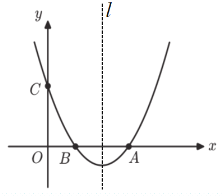
【題目】如圖,在平面直角坐標系中,拋物線![]() 與x軸交于點A,B(1,0),與
與x軸交于點A,B(1,0),與![]() 軸交于點C(0,3),對稱軸為直線
軸交于點C(0,3),對稱軸為直線![]() .
.
(1)求拋物線的解析式及點A的坐標;
(2)在對稱軸![]() 上是否存在一點M,使得△BCM周長最小?若存在,求出△BCM周長;若不存在,請說明理由;
上是否存在一點M,使得△BCM周長最小?若存在,求出△BCM周長;若不存在,請說明理由;
(3)若點P是拋物線上一動點,從點C沿拋物線向點A運動,過點P作PD//![]() 軸,交AC于點D,當△ADP是直角三角形時,求點P的坐標.
軸,交AC于點D,當△ADP是直角三角形時,求點P的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖(1),在正方形ABCD中,點E是AB邊上的一個動點(點E與點A,B不重合),連接CE,過點B作![]() 于點G,交AD于點F.
于點G,交AD于點F.
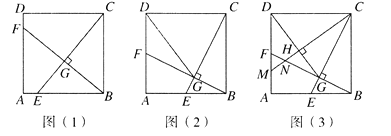
(1)求證:![]() ;
;
(2)如圖(2),當點E運動到AB的中點時,連接DG,求證:![]() ;
;
(3)如圖(3),在(2)的條件下,過點C作![]() 于點H,分別交AD,BF于點M,N,求證:
于點H,分別交AD,BF于點M,N,求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(2014河南22題)
(1)問題發(fā)現(xiàn)
如圖①,![]() 和
和![]() 均為等邊三角形,點A、D、E在同一條直線上,連接BE;
均為等邊三角形,點A、D、E在同一條直線上,連接BE;
填空:
①![]() 的度數(shù)為__________;
的度數(shù)為__________;
②線段AD、BE之間的數(shù)量關系為__________.
(2)拓展探究
如圖②,![]() 和
和![]() 均為等腰直角三角形,
均為等腰直角三角形,![]() ,點A、D、E在同一條直線上,CM為
,點A、D、E在同一條直線上,CM為![]() 中DE邊上的高,連接BE.請判斷
中DE邊上的高,連接BE.請判斷![]() 的度數(shù)及線段CM、AE、BE之間的數(shù)量關系,并說明理由;
的度數(shù)及線段CM、AE、BE之間的數(shù)量關系,并說明理由;
(3)解決問題
如圖③,在正方形ABCD中,![]() ,若點P滿足
,若點P滿足![]() ,且
,且![]() ,請直接寫出點A到BP的距離.
,請直接寫出點A到BP的距離.
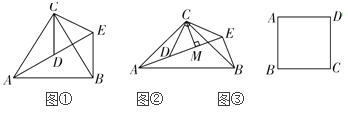
圖① 圖② 圖③
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,過點A且與x軸平行的直線交拋物線y=![]() (x+1)2于B,C兩點,若線段BC的長為6,則點A的坐標為( )
(x+1)2于B,C兩點,若線段BC的長為6,則點A的坐標為( )
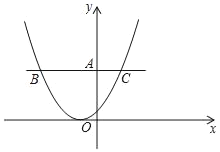
A.(0,1)B.(0,4.5)C.(0,3)D.(0,6)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com