
【題目】某商店需要購進甲、乙兩種商品共1000件,其進價和售價如下表所示:
甲 | 乙 | |
進價(元/件) | 15 | 35 |
售價(元/件) | 18 | 44 |
(1)若商店計劃銷售完這批商品后能獲利4200元,則甲、乙兩種商品應分別購進多少件;
(2)若該商店銷售完這批商品后獲利要多于5000元,則至少應購進乙種商品多少件?
【答案】(1)購進甲種商品800件,購進乙種商品200件;(2)334;
【解析】
(1)設購進甲種商品x件,購進乙種商品y件,根據購進甲乙兩種商品共1000件及銷售完這批商品后能獲利4200元,即可得出關于x、y的二元一次方程組,解之即可得出結論;
(2)設購進乙種商品a件,則購進甲種商品(1000-a)件,根據總利潤=單件利潤×購進數量結合該商店銷售完這批商品后獲利要多于5000元,即可得出關于a的一元一次不等式,解之取其中的最小的整數即可得出結論.
解:(1)設購進甲種商品x件,購進乙種商品y件,
根據題意得: ,
,
解得:![]() ,
,
則購進甲種商品800件,購進乙種商品200件,
答:購進甲種商品800件,購進乙種商品200件;
(2)設購進乙種商品a件,則購進甲種商品(1000-a)件,
根據題意得:(44-35)a+(18-15)(1000-a)>5000,
解得:![]() ,
,
∵a為整數,
∴a的最小值為334.
答:至少應購進乙種商品334件.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:初中數學 來源: 題型:
【題目】如圖,LA,LB分別表示A步行與B騎車在同一路上行駛的路程y(千米)與時間x(小時)的關系.根據圖象,回答下列問題:

(1)B出發時與A相距 千米.
(2)B騎車一段路后,自行車發生故障,進行修理,所用的時間是 小時.
(3)B出發后 小時與A相遇.
(4)求出A行走的路程y與時間x的函數關系式.(寫出過程)
(5)若B的自行車不發生故障,保持出發時的速度勻速行駛,A,B肯定會提前相遇.在圖中畫出這種假設情況下B騎車行駛過程中路程y與時間x的函數圖象,在圖中標出這個相遇點P,并回答相遇點P離B的出發點O相距多少千米.(寫出過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() 是坐標原點,四邊形
是坐標原點,四邊形![]() 是菱形,點
是菱形,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸的負半軸上,直線
軸的負半軸上,直線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() 邊交
邊交![]() 軸于點
軸于點![]() .
.
(1)如圖1,求直線![]() 的解析式;
的解析式;

(2)如圖2,連接![]() ,動點
,動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 方向以1個單位/秒的速度向終點
方向以1個單位/秒的速度向終點![]() 勻速運動,設
勻速運動,設![]() 的面積為
的面積為![]() (
(![]() ),點
),點![]() 的運動時間為
的運動時間為![]() 秒,求
秒,求![]() 與
與![]() 之間的函數關系式,并直接寫出自變量
之間的函數關系式,并直接寫出自變量![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】復雜的數學問題我們常會把它分解為基本問題來研究,化繁為簡,化整為零這是一種常見的數學解題思想.
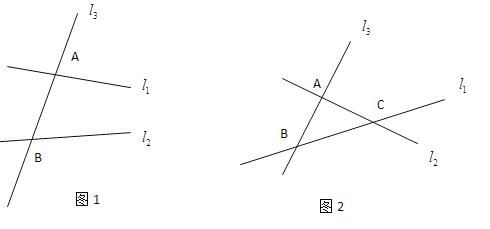
(1)如圖1,直線![]() ,
,![]() 被直線
被直線![]() 所截,在這個基本圖形中,形成了______對同旁內角.
所截,在這個基本圖形中,形成了______對同旁內角.
(2)如圖2,平面內三條直線![]() ,
,![]() ,
,![]() 兩兩相交,交點分別為
兩兩相交,交點分別為![]() 、
、![]() 、
、![]() ,圖中一共有______對同旁內角.
,圖中一共有______對同旁內角.
(3)平面內四條直線兩兩相交,最多可以形成______對同旁內角.
(4)平面內![]() 條直線兩兩相交,最多可以形成______對同旁內角.
條直線兩兩相交,最多可以形成______對同旁內角.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】假山具有多方面的造景功能,與建筑、植物等組合成富于變化的景致.某公園有一座假山,小亮、小慧等同學想用一些測量工具和所學的幾何知識測量這座假山的高度來檢驗自己掌握知識和運用知識的能力,如圖,在陽光下,小亮站在水平地面的D處,此時小亮身高的影子頂端與假山的影子頂端E重合,這時小亮身高CD的影長DE=2米,一段時間后,小亮從D點沿BD的方向走了3.6米到達G處,此時小亮身高的影子頂端與假山的影子頂端H重合,這時小亮身高的影長GH=2.4米,已知小亮的身高CD=FG=1.5米,點G,E,D均在直線BH上,AB⊥BH,CD⊥BH,GF⊥BH,請你根據題中提供的相關信息,求出假山的高度AB.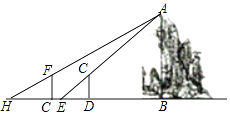
查看答案和解析>>
科目:初中數學 來源: 題型:
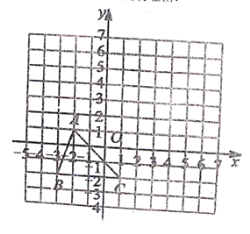
【題目】已知:如圖把![]() 向上平移3個單位長度,再向右平移2個單位長度,得到
向上平移3個單位長度,再向右平移2個單位長度,得到![]() .
.
(1)在圖中畫出![]() ;
;
(2)寫出點![]() 的坐標:
的坐標:![]() 的坐標為______,
的坐標為______,![]() 的坐標為 _________;
的坐標為 _________; ![]() 的坐標為________.
的坐標為________.
(3)在![]() 軸上是否存在一點P,使得
軸上是否存在一點P,使得![]() 的面積相等?若存在,請求出點P的坐標;若不存在,說明理由.
的面積相等?若存在,請求出點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古代數學的許多發現都曾位居世界前列,其中“楊輝三角”就是一例.如圖,這個三角形的構造法則:兩腰上的數都是1,其余每個數均為其上方左右兩數之和,它給出了![]() (n為正整數)的展開式(按a的次數由大到小的順序排列)的系數規律.例如,在三角形中第三行的三個數1,2,1,恰好對應
(n為正整數)的展開式(按a的次數由大到小的順序排列)的系數規律.例如,在三角形中第三行的三個數1,2,1,恰好對應![]() 展開式中的系數;第四行的四個數1,3,3,1,恰好對應著
展開式中的系數;第四行的四個數1,3,3,1,恰好對應著![]() 展開式中的系數等等.
展開式中的系數等等.

(1)根據上面的規律,寫出![]() 的展開式.
的展開式.
(2)利用上面的規律計算:![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小明想測山高和索道的長度.他在B處仰望山頂A,測得仰角∠B=31°,再往山的方向(水平方向)前進80m至索道口C處,沿索道方向仰望山頂,測得仰角∠ACE=39°.
(1)求這座山的高度(小明的身高忽略不計);
(2)求索道AC的長(結果精確到0.1m).
(參考數據:tan31°≈ ![]() ,sin31°≈
,sin31°≈ ![]() ,tan39°≈
,tan39°≈ ![]() ,sin39°≈
,sin39°≈ ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() 、
、![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,其中
,其中![]() ,
,![]() 滿足
滿足![]() .將點
.將點![]() 向右平移
向右平移![]() 個單位長度得到點
個單位長度得到點![]() ,如圖所示.
,如圖所示.

(1)求點![]() ,
,![]() ,
,![]() 的坐標;
的坐標;
(2)動點![]() 從點
從點![]() 出發,沿著線段
出發,沿著線段![]() 、線段
、線段![]() 以
以![]() 個單位長度/秒的速度運動,同時點
個單位長度/秒的速度運動,同時點![]() 從點
從點![]() 出發沿著線段
出發沿著線段![]() 以
以![]() 個單位長度秒的速度運動,設運動時間為
個單位長度秒的速度運動,設運動時間為![]() 秒
秒![]() .當
.當![]() 時,求
時,求![]() 的取值范圍;是否存在一段時間,使得
的取值范圍;是否存在一段時間,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com