

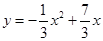 ;(2)C
;(2)C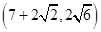 ;(3)(3,9)和(
;(3)(3,9)和(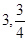 );
);
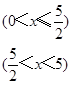 ,當
,當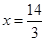 時,y最大且最大值為
時,y最大且最大值為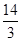 .
.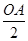 =
=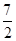 時,點D剛好在OA上,分①當0<x≤
時,點D剛好在OA上,分①當0<x≤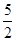 時,②當
時,②當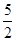 <x<5時,根據相似三角形的性質及二次函數的性質求解即可.
<x<5時,根據相似三角形的性質及二次函數的性質求解即可.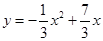 ;
;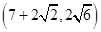 ;
;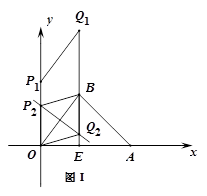
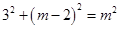 ,解得
,解得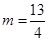 ,求得Q2為(
,求得Q2為(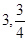 );綜上所述滿足條件的Q點有(3,9)和(
);綜上所述滿足條件的Q點有(3,9)和(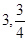 );
);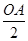 =
=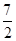 時,點D剛好在OA上,所以分兩種情況考慮:
時,點D剛好在OA上,所以分兩種情況考慮: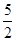 時,△DMN≌△BMN,△BMN∽△BOA,而
時,△DMN≌△BMN,△BMN∽△BOA,而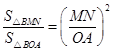 ,計算得
,計算得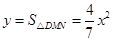 ;
;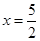 時,y最大且最大值為
時,y最大且最大值為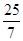 .
.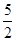 <x<5時,連結BD交MN于F、交OA于G,DM交OA于H,DN交OA于I,
<x<5時,連結BD交MN于F、交OA于G,DM交OA于H,DN交OA于I,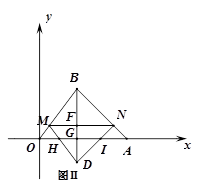
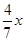 ,FG=4-
,FG=4-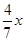 ,DG=DF-FG=
,DG=DF-FG=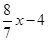 ,
,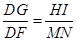 ,計算得HI=
,計算得HI=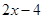 ,
,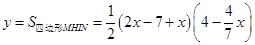 =
=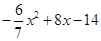 ,
,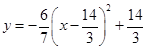 ;當
;當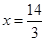 時,y最大且最大值為
時,y最大且最大值為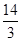 .
.
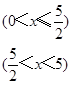 ,當
,當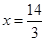 時,y最大且最大值為
時,y最大且最大值為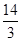 .
.

 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
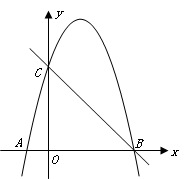
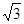 ),點D的坐標為(1,
),點D的坐標為(1,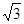 ),點C在
),點C在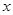 軸的正半軸上,過點O且以點D為頂點的拋物線經過點C,點P為CD的中點.
軸的正半軸上,過點O且以點D為頂點的拋物線經過點C,點P為CD的中點.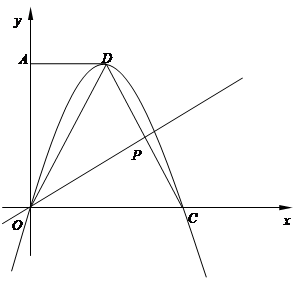
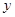 軸右側的拋物線上是否存在點Q,使以Q為圓心的圓同時與
軸右側的拋物線上是否存在點Q,使以Q為圓心的圓同時與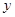 軸、直線OP相切.若存在,請求出滿足條件的點Q的坐標;若不存在,請說明理由;
軸、直線OP相切.若存在,請求出滿足條件的點Q的坐標;若不存在,請說明理由;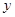 軸的正半軸交于點N.求證:OM+ON為定值.
軸的正半軸交于點N.求證:OM+ON為定值.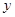 軸上找一點H,使∠PHD最大.試求出點H的坐標.
軸上找一點H,使∠PHD最大.試求出點H的坐標.查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.3 | B.5 | C.7 | D.不確定 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.y=(x-2) 2+1 | B.y=(x-2) 2-1 |
| C.y=(x+2) 2+1 | D.y=(x+2) 2-1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com