
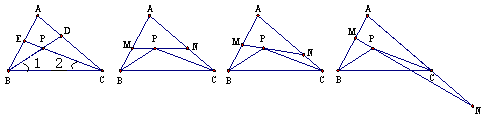
 ∠A;(3)∠MPB+∠NPC= 90°-
∠A;(3)∠MPB+∠NPC= 90°- ∠A,∠MPB-∠NPC=90°-
∠A,∠MPB-∠NPC=90°- ∠A.
∠A. ∠A;
∠A; ∠A,則∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A,則∠MPB+∠NPC=180°-∠BPC=180°-(90°+ ∠A)= 90°-
∠A)= 90°- ∠A;(ⅱ)不成立,∠MPB-∠NPC=90°-
∠A;(ⅱ)不成立,∠MPB-∠NPC=90°- ∠A.理由:由圖可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+
∠A.理由:由圖可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+ ∠A,因此∠MPB-∠NPC=180°-∠BPC=180°-(90°+
∠A,因此∠MPB-∠NPC=180°-∠BPC=180°-(90°+ ∠A)= 90°-
∠A)= 90°- ∠A.
∠A. ∠ABC,
∠ABC, ∠ACB,
∠ACB, (∠ABC+∠ACB)
(∠ABC+∠ACB) ×110°=55°,
×110°=55°, ∠A,
∠A, ∠A)=90°-
∠A)=90°- ∠A;
∠A; ∠A.
∠A. ∠A,則∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A,則∠MPB+∠NPC=180°-∠BPC=180°-(90°+ ∠A)= 90°-
∠A)= 90°- ∠A;
∠A; ∠A(1分).
∠A(1分). ∠A,
∠A, ∠A)= 90°-
∠A)= 90°- ∠A.
∠A.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 .
.
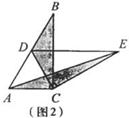
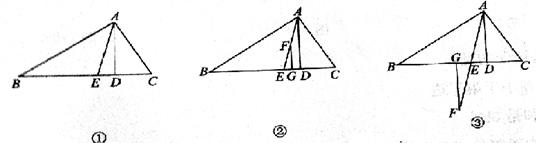
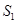 ,△AEC的面積為
,△AEC的面積為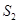 。則
。則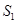 與
與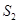 的數量關系是 。
的數量關系是 。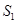 與
與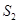 的數量關系仍然成立,并嘗試分別作出了△BDC,△AEC中
的數量關系仍然成立,并嘗試分別作出了△BDC,△AEC中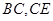 邊上的高,請你證明小明的猜想。
邊上的高,請你證明小明的猜想。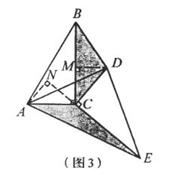
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 ,
,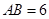 ,
,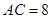 ,點
,點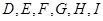 都是矩形
都是矩形 的邊上,則矩形
的邊上,則矩形 的面積為( )
的面積為( )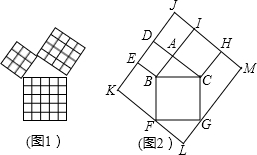
A.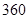 | B. | C.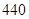 | D.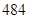 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題

A.10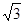 -15 -15 | B.10-5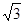 |
C.5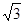 -5 -5 | D.20-10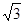 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
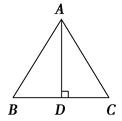
| A.AB=AC |
| B.∠BAC=90° |
| C.BD=AC |
| D.∠B=45° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com