
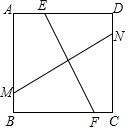
 如圖,正方形ABCD內(nèi)有兩條相交線段MN、EF,M、N、E、F分別在邊AB、C D、A D、BC上.小明認(rèn)為:若MN=EF,則MN⊥EF;小亮認(rèn)為:若MN丄EF,則MN=EF,你認(rèn)為( )
如圖,正方形ABCD內(nèi)有兩條相交線段MN、EF,M、N、E、F分別在邊AB、C D、A D、BC上.小明認(rèn)為:若MN=EF,則MN⊥EF;小亮認(rèn)為:若MN丄EF,則MN=EF,你認(rèn)為( )| A. | 兩人都對(duì) | B. | 僅小亮對(duì) | C. | 僅小明對(duì) | D. | 兩人都不對(duì) |
分析 分別過點(diǎn)E作EG⊥BC于點(diǎn)G,過點(diǎn)M作MP⊥CD于點(diǎn)P,設(shè)EF與MN相交于點(diǎn)O,MP與EF相交于點(diǎn)Q,根據(jù)正方形的性質(zhì)可得EG=MP,對(duì)小明同學(xué)的說法,先利用“HL”證明Rt△EFG和Rt△MNP全等,根據(jù)全等三角形對(duì)應(yīng)角相等可得∠MNP=∠EFG,再根據(jù)角的關(guān)系推出∠EQM=∠MNP,然后根據(jù)∠MNP+∠NMP=90°得到∠NMP+∠EQM=90°,從而得到∠MOQ=90°,根據(jù)垂直的定義,MN⊥EF,當(dāng)E向D移動(dòng),F(xiàn)向B移動(dòng),同樣使MN=EF,此時(shí)就不垂直;對(duì)小亮同學(xué)的說法,先推出∠EQM=∠EFG,∠EQM=∠MNP,然后得到∠EFG=∠MNP,然后利用“角角邊”證明△EFG和△MNP全等,根據(jù)全等三角形對(duì)應(yīng)邊相等可得EF=MN.
解答 解:如圖,過點(diǎn)E作EG⊥BC于點(diǎn)G,過點(diǎn)M作MP⊥CD于點(diǎn)P,設(shè)EF與MN相交于點(diǎn)O,MP與EF相交于點(diǎn)Q,
∵四邊形ABCD是正方形,
∴EG=MP,
對(duì)同學(xué)小明的說法:
在Rt△EFG和Rt△MNP中,
$\left\{\begin{array}{l}{MN=EF}\\{EG=MP}\end{array}\right.$,
∴Rt△EFG≌Rt△MNP(HL),
∴∠MNP=∠EFG,
∵M(jìn)P⊥CD,∠C=90°,
∴MP∥BC,
∴∠EQM=∠EFG=∠MNP,
又∵∠MNP+∠NMP=90°,
∴∠EQM+∠NMP=90°,
在△MOQ中,∠MOQ=180°-(∠EQM+∠NMP)=180°-90°=90°,
∴MN⊥EF,
當(dāng)E向D移動(dòng),F(xiàn)向B移動(dòng),同樣使MN=EF,此時(shí)就不垂直,
故小明不正確.
對(duì)乙同學(xué)的說法:∵M(jìn)P⊥CD,∠C=90°,
∴MP∥BC,
∴∠EQM=∠EFG,
∵M(jìn)N⊥EF,
∴∠NMP+∠EQM=90°,
又∵M(jìn)P⊥CD,
∴∠NMP+∠MNP=90°,
∴∠EQM=∠MNP,
∴∠EFG=∠MNP,
在△EFG和△MNP中,
$\left\{\begin{array}{l}{∠EFG=∠MNP}\\{∠EGF=∠MPN=90°}\\{EG=MP}\end{array}\right.$,
∴△EFG≌△MNP(AAS),
∴MN=EF,故小亮同學(xué)的說法正確,
綜上所述,僅小亮同學(xué)的說法正確.
故選B.
點(diǎn)評(píng) 本題考查了正方形的性質(zhì),全等三角形的判定與性質(zhì),同角的余角相等的性質(zhì),作出輔助線,構(gòu)造出全等三角形是解題的關(guān)鍵,通常情況下,求兩邊相等,或已知兩邊相等,都是想法把這兩條線段轉(zhuǎn)化為全等三角形的對(duì)應(yīng)邊進(jìn)行求解.


 一線名師提優(yōu)試卷系列答案
一線名師提優(yōu)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 五邊形 | B. | 六邊形 | C. | 七邊形 | D. | 八邊形 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 有一個(gè)數(shù)值轉(zhuǎn)換器,程序如圖,當(dāng)輸入的x為25時(shí),輸出的y是( )
有一個(gè)數(shù)值轉(zhuǎn)換器,程序如圖,當(dāng)輸入的x為25時(shí),輸出的y是( )| A. | 5 | B. | -5 | C. | $\sqrt{5}$ | D. | -$\sqrt{5}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 一樣 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com