
【題目】如圖,在四邊形ABCD中,AB=BC,對角線BD平分∠ABC,P是BD上一點,過點P作PM⊥AD,PN⊥CD,垂足分別為M,N.
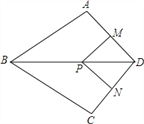
(1)求證:∠ADB=∠CDB;
(2)若∠ADC=90°,求證:四邊形MPND是正方形.
【答案】(1)(2)證明見解析
【解析】試題分析:(1)根據角平分線的性質和全等三角形的判定方法證明△ABD≌△CBD,由全等三角形的性質即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的條件可得四邊形MPND是矩形,再根據兩邊相等的四邊形是正方形即可證明四邊形MPND是正方形.
證明:(1)∵對角線BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
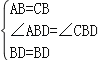 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四邊形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四邊形MPND是正方形.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖①是棱長為a的小正方體,如圖②、如圖③是由若干這樣相同的小正方體擺放而成,按照這樣的方法繼續擺放,由上而下分別叫第一層、第二層、…、第n層,第n層中小正方體的個數為s(提示:第一層中,s=1;第二層中,s=3),則第n層中,s=________.(用含n的式子表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=2 ![]() ,以點C為圓心,CB的長為半徑畫弧,與AB邊交于點D,將
,以點C為圓心,CB的長為半徑畫弧,與AB邊交于點D,將 ![]() 繞點D旋轉180°后點B與點A恰好重合,則圖中陰影部分的面積為
繞點D旋轉180°后點B與點A恰好重合,則圖中陰影部分的面積為 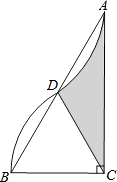
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某儲運部緊急調撥一批物資,調進物資共用4小時,調進物資2小時后開始調出物資(調進物資與調出物資的進度均保持不變).儲運部庫存物資w(噸)與時間t(小時)之間的函數關系如圖所示,請問這批物資從開始調進到全部調出需要多長時間?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,直線
,直線![]() ,垂足為O,直線PQ經過點O,且
,垂足為O,直線PQ經過點O,且![]() 點B在直線l上,位于點O下方,
點B在直線l上,位于點O下方,![]() 點C在直線PQ上運動
點C在直線PQ上運動![]() 連接BC過點C作
連接BC過點C作![]() ,交直線MN于點A,連接
,交直線MN于點A,連接![]() 點A、C與點O都不重合
點A、C與點O都不重合![]() .
.
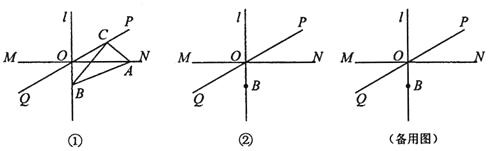
![]() 小明經過畫圖、度量發現:在
小明經過畫圖、度量發現:在![]() 中,始終有一個角與
中,始終有一個角與![]() 相等,這個角是________________;
相等,這個角是________________;
![]() 當
當![]() 時,在圖
時,在圖![]() 中畫出示意圖并證明
中畫出示意圖并證明![]() ;
;
![]() 探索
探索![]() 和
和![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖.在直角坐標系中,矩形ABCO的邊OA在x軸上,邊OC在y軸上,點B的坐標為(1,3),將矩形沿對角線AC翻折,B點落在D點的位置,且AD交y軸于點E.那么點D的坐標為( ) 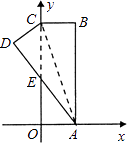
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校計劃購買A、B兩種品牌的顯示器共120臺,A、B兩種品牌顯示器的單價分別為800元和1000元,設購買A品牌顯示器x臺,若學校購買這兩種品牌顯示器的總費用為110000元,那么A、B兩種品牌的顯示器各購買了多少臺?根據題目信息完成上面的表格,并列出方程,列出的方程: .
項目品牌 | 單價/元 | 購買數量/臺 | 購買費用/元 |
A | 800 | x |
|
B | 1000 |
|
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛貨車和一輛小轎車同時從甲地出發,貨車勻速行駛至乙地,小轎車中途停車休整2h后提速行駛至乙地.設行駛時間為x( h),貨車的路程為y1( km),小轎車的路程為y2( km ),圖中的線段OA與折線OBCD分別表示y1,y2與x之間的函數關系.
(1)甲乙兩地相距_____km,m=_____;
(2)求線段CD所在直線的函數表達式;
(3)小轎車停車休整后還要提速行駛多少小時,與貨車之間相距20km?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com