
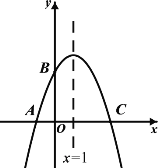
【題目】如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸的一個交點為A(-1,0),對稱軸為直線x =1,與y軸的交點B在(0,2)和(0,3)之間(包括這兩點),下列四個結論中,①當x>3時,y<0;② 3a+b<0;③-1≤a ≤![]() ;④4ac-b2> 8a;所有正確結論的序號是_______________ .
;④4ac-b2> 8a;所有正確結論的序號是_______________ .
【答案】①②③
【解析】
由拋物線的對稱性可求得拋物線與x軸另一個交點的坐標,據此可判斷①;
根據拋物線的對稱軸為直線x=1可得a與b的關系式,再結合a為負數即而可判斷②;
設拋物線的解析式為![]() ,根據拋物線與y軸的交點B在(0,2)和(0,3)之間可得關于a的不等式,解不等式即可判斷③;
,根據拋物線與y軸的交點B在(0,2)和(0,3)之間可得關于a的不等式,解不等式即可判斷③;
根據拋物線y軸的交點B在(0,2)和(0,3)之間,可得c的取值范圍,再假設④正確,則可推出c的相應范圍,由此可判斷④.
解:由拋物線的對稱性可求得拋物線與x軸另一個交點的坐標為(3,0),所以當x>3時,y<0,故①正確;
因為拋物線開口向下,所以a<0,∵![]() =1,∴2a+b=0,∴
=1,∴2a+b=0,∴![]() ,故②正確;
,故②正確;
設拋物線的解析式為![]() ,則
,則![]() ,令x=0,得:
,令x=0,得:![]() ,
,
∵拋物線與y軸的交點B在(0,2)和(0,3)之間,∴![]() ,解得:
,解得:![]() ,故③正確;
,故③正確;
∵拋物線與y軸的交點B在(0,2)和(0,3)之間,∴2≤c≤3,
若![]() ,則
,則![]() ,∵a<0,∴
,∵a<0,∴![]() ,∴
,∴![]() ,∴c<2,與2≤c≤3矛盾,故④錯誤.
,∴c<2,與2≤c≤3矛盾,故④錯誤.
故答案為:①②③.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程![]() (m為常數)
(m為常數)
(1)求證:不論m為何值,方程總有兩個不相等的實數根;
(2)若方程有一個根是2,求m的值及方程的另一個根。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】射線QN與等邊△ABC的兩邊AB,BC分別交于點M,N,且AC∥QN,AM=MB=2cm,QM=4cm.動點P從點Q出發,沿射線QN以每秒1cm的速度向右移動,經過t秒,以點P為圓心,![]() cm為半徑的圓與△ABC的邊相切(切點在邊上),請寫出t可取的一切值 (單位:秒)
cm為半徑的圓與△ABC的邊相切(切點在邊上),請寫出t可取的一切值 (單位:秒)
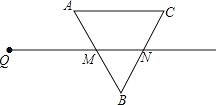
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某通訊器材公司銷售一種市場需求較大的新型通訊產品,已知每件產品的進價為40元,每年銷售該種產品的總開支(不含進價)為120萬元,在銷售過程中發現,年銷售量![]() (萬件)與銷售單價
(萬件)與銷售單價![]() (元)之間存在著如圖所示的一次函數關系.
(元)之間存在著如圖所示的一次函數關系.
⑴ 直接寫出![]() 關于
關于![]() 的函數關系式為 .
的函數關系式為 .
⑵ 市場管理部門規定,該產品銷售單價不得超過100元,該公司銷售該種產品當年獲利55萬元,求當年的銷售單價.

查看答案和解析>>
科目:初中數學 來源: 題型:
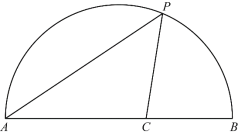
【題目】如圖,點P是![]() 上一動點,連接AP,作∠APC=45°,交弦AB于點C.已知AB=6cm,設A,P兩點間的距離為xcm,P,C兩點間的距離為y1cm,A,C兩點間的距離為y2cm.(當點P與點A重合時,y1,y2的值為0;當點P與點B重合時,y1的值為0,y2的值為6).
上一動點,連接AP,作∠APC=45°,交弦AB于點C.已知AB=6cm,設A,P兩點間的距離為xcm,P,C兩點間的距離為y1cm,A,C兩點間的距離為y2cm.(當點P與點A重合時,y1,y2的值為0;當點P與點B重合時,y1的值為0,y2的值為6).
小智根據學習函數的經驗,分別對函數y隨自變量x的變化而變化的規律進行了探究.
下面是小智的探究過程,請補充完整:
(1)按照下表中自變量x的值進行取點、畫圖、測量,分別得到了y與x的幾組對應值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 1.21 | 2.09 | m | 2.99 | 2.82 | 0 |
y2/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6 |
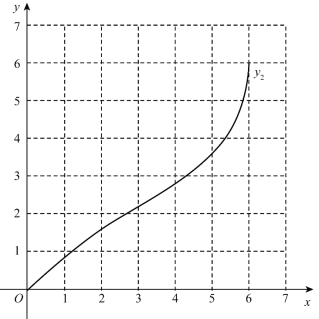
經測量m的值是 (保留一位小數).
(2)在同一平面直角坐標系xOy中,描出補全后的表中各組數值所對應的點(x,y1),(x,y2),并畫出函數yspan>1,y2的圖象;
(3)結合函數圖象,解決問題:當△ACP為等腰三角形時,AP的長度約為 cm(保留一位小數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數學課上,老師提出利用尺規作圖完成下面問題:

小明的作法如下:

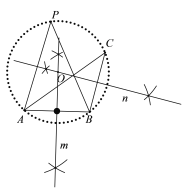
老師說:“小明的作法正確.”
請回答:(1)點O為△ABC外接圓圓心(即OA=OB=OC)的依據是____;
(2)∠APB=∠ACB的依據是______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面內,C為線段AB外的一點,若以A,B,C為頂點的三角形為直角三角形,則稱C為線段AB的直角點. 特別地,當該三角形為等腰直角三角形時,稱C為線段AB的等腰直角點.
(1)如圖1,在平面直角坐標系xOy中,點M的坐標為![]() ,在點P1
,在點P1![]() ,P2
,P2![]() ,P3
,P3![]() 中,線段OM的直角點是 ;
中,線段OM的直角點是 ;
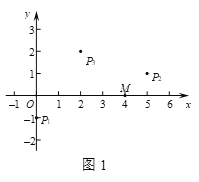
(2)在平面直角坐標系xOy中,點A,B的坐標分別為![]() ,
,![]() ,直線l的解析式為
,直線l的解析式為![]() .
.
①如圖2,C是直線l上的一個動點,若C是線段AB的直角點,求點C的坐標;
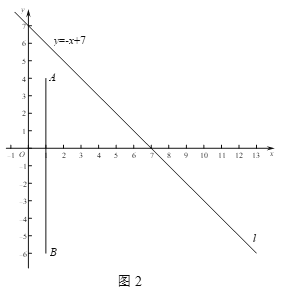
②如圖3,P是直線l上的一個動點,將所有線段AP的等腰直角點稱為直線l關于點A的伴隨點.若⊙O的半徑為r,且⊙O上恰有兩個點為直線l關于點A的伴隨點,直接寫出r的取值范圍.
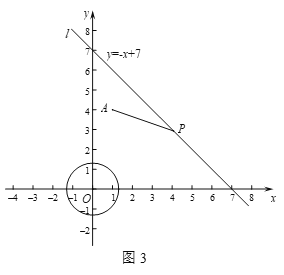
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com