
【題目】如圖,四邊形![]() 是以原點
是以原點![]() 為對稱中心的矩形,
為對稱中心的矩形,![]() ,
,![]() ,
,![]() 和
和![]() 分別與
分別與![]() 軸交于點
軸交于點![]() 、
、![]() ,連接
,連接![]() .
.

(1)寫出點![]() 和點
和點![]() 的坐標;
的坐標;
(2)求四邊形![]() 的面積;
的面積;
(3)判斷點![]() 在矩形
在矩形![]() 的內部還是外部;
的內部還是外部;
(4)要使直線![]() 與矩形
與矩形![]() 沒有公共點,直接寫出
沒有公共點,直接寫出![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)5;(3)點
;(2)5;(3)點![]() 在矩形的內部;(4)
在矩形的內部;(4) ![]() 或
或![]()
【解析】
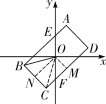
解:(1)∵四邊形ABCD是以原點O為對稱中心的矩形,
∴點A和點C、點B和點D關于原點對稱,
∵![]() ,
,![]()
∴![]() ,
,![]() ;
;
(2)設直線CD的解析式為![]() ,
,
將點C、D的坐標分別代入![]() 得
得![]() ,
,
解得![]() ,
,
∴直線CD的解析式為![]() ,
,
當![]() 時,
時,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
如解圖,過點O作![]() 、
、![]() ,垂足分別為點M、N,
,垂足分別為點M、N,
∵四邊形ABCD為矩形,
∴![]() ,
,![]() ,
,
如解圖,連接OC,
∴![]() ;
;
(3)在直線CD的解析式![]() 上,當
上,當![]() 時,
時,![]() ,
,
∵![]() ,
,
∴點![]() 在點
在點![]() 的上方,
的上方,
又∵![]() ,
,
∴點![]() 在矩形的內部;
在矩形的內部;
(4) ![]() 或
或![]() .
.
【解法提示】當直線![]() 過A或C點時,直線與矩形只有一個公共點,
過A或C點時,直線與矩形只有一個公共點,
把![]() 代入
代入![]() ,得
,得![]() ,解得
,解得![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴當直線![]() 與矩形ABCD沒有公共點時,m的取值范圍為
與矩形ABCD沒有公共點時,m的取值范圍為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,扇形OAB中,∠AOB=100°,OA=12,C是OB的中點,CD⊥OB交![]() 于點D,以OC為半徑的
于點D,以OC為半徑的![]() 交OA于點E,則圖中陰影部分的面積是( )
交OA于點E,則圖中陰影部分的面積是( )

A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
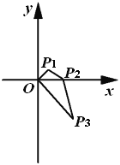
【題目】如圖,在平面直角坐標系中,點![]() 的坐標
的坐標 ,將線段
,將線段![]() 繞點
繞點![]() 按順時針方向旋轉45°,再將其長度伸長為
按順時針方向旋轉45°,再將其長度伸長為![]() 的2倍,得到線段
的2倍,得到線段![]() ;又將線段
;又將線段![]() 繞點
繞點![]() 按順時針方向旋轉45°,長度伸長為
按順時針方向旋轉45°,長度伸長為![]() 的2倍,得到線段
的2倍,得到線段![]() ;如此下去,得到線段
;如此下去,得到線段![]() 、
、![]() ,……,
,……,![]() (
(![]() 為正整數),則點
為正整數),則點![]() 的坐標是_________.
的坐標是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
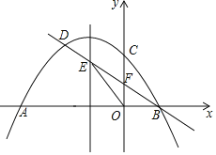
【題目】如圖,拋物線![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,過點B的直線與拋物線的另一個交點為D,與拋物線的對稱軸交于點E,與y軸交于點F,且
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,過點B的直線與拋物線的另一個交點為D,與拋物線的對稱軸交于點E,與y軸交于點F,且![]() ,△OBE的面積為
,△OBE的面積為![]() .
.
(1)求拋物線的解析式;
(2)設P為已知拋物線上的任意一點,當△ACP的面積等于△ACB的面積時,求點P的坐標;
(3)點Q(0,m)是y軸上的動點,連接AQ、BQ,當∠AQB為鈍角時,則m的取值范圍是 .(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角坐標系xOy中,一次函數y=﹣![]() x+5的圖象l1分別與x,y軸交于A,B兩點,正比例函數的圖象l2與l1交于點C(m,4).
x+5的圖象l1分別與x,y軸交于A,B兩點,正比例函數的圖象l2與l1交于點C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函數y=kx+1的圖象為l3,且11,l2,l3不能圍成三角形,直接寫出k的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2﹣ax﹣2a(a為常數且不等于0)與x軸的交點為A,B兩點,且A點在B的右側.
(1)當拋物線經過點(3,8),求a的值;
(2)求A、B兩點的坐標;
(3)若拋物線的頂點為M,且點M到x軸的距離等于AB的3倍,求拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是根據某市2010年至2014年工業生產總值繪制的折線統計圖,觀察統計圖獲得以下信息,其中信息判斷錯誤的是( )

A.2010年至2014年間工業生產總值逐年增加
B.2014年的工業生產總值比前一年增加了40億元
C.2012年與2013年每一年與前一年比,其增長額相同
D.從2011年至2014年,每一年與前一年比,2014年的增長率最大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】假期里,小紅和小惠去買菜,三次購買的西紅柿價格和數量如下表:
單價/(元/千克) | 4 | 3 | 2 | 合計 |
小紅購買的數量/千克 | 1 | 2 | 3 | 6 |
小惠購買的數量/千克 | 2 | 2 | 2 | 6 |
(1)小紅和小惠購買西紅柿數量的中位數、眾數是多少?
(2)從平均價格看,誰買的西紅柿要便宜些.請思考下面小亮和小明的說法,你認為誰說得對?為什么?
小亮的說法
每次購買單價相同,購買總量也相同,平均價格應該也一樣,都是![]() (元/千克),所以兩人購買的西紅柿一樣便宜.
(元/千克),所以兩人購買的西紅柿一樣便宜.
小明的說法
購買的總量雖然相同,但小紅花了16元,小惠花了18元,平均價格不一樣,所以小紅購買的西紅柿便宜.
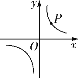
(3)小明在直角坐標系中畫出反比例函數的圖象,圖象經過點![]() (如圖),點
(如圖),點![]() 的橫、縱坐標分別為小紅和小惠購買西紅柿價格的平均數.
的橫、縱坐標分別為小紅和小惠購買西紅柿價格的平均數.
①求此反比例函數的關系式;
②判斷點![]() 是否在此函數圖象上.
是否在此函數圖象上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com