
 如下數表是由從1開始的連續自然數組成的,則第10行各數之和1729.
如下數表是由從1開始的連續自然數組成的,則第10行各數之和1729. 分析 由數列知第n行最后一數為n2,則第一個數為n2-2n+2,每行數的個數為1,3,5,…的奇數列,從而得第n行各數之和為$\frac{{n}^{2}-2n+2+{n}^{2}}{2}$×(2n-1)=(n2-n+1)(2n-1),將n=10代入以上列式從而解得.
解答 解:第n行最后一數為n2,則第一個數為n2-2n+2,
每行數由題意知每行數的個數為1,3,5,…的奇數列,
第n行共有2n-1個;
第n行各數之和:$\frac{{n}^{2}-2n+2+{n}^{2}}{2}$×(2n-1)=(n2-n+1)(2n-1).
當n=10時,(n2-n+1)(2n-1)=(102-10+1)(2×10-1)=1729,
故答案為:1729.
點評 此題考查數字變化的規律,通過觀察,分析、歸納并發現規律:每行最后一個數為行數的平方,每行數的個數是行數的2倍與1的差是本題的關鍵.


科目:初中數學 來源: 題型:解答題
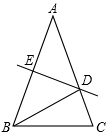 如圖,在△ABC中,AB=AC=5,AB的垂直平分線DE分別交AB、AC于E、D兩點.
如圖,在△ABC中,AB=AC=5,AB的垂直平分線DE分別交AB、AC于E、D兩點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
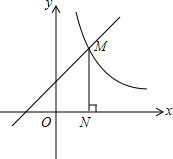 如圖,一次函數y=x+1的圖象與反比例函數y=$\frac{k}{x}$(x>0)的圖象交于點M,作MN⊥x軸,N為垂足,且ON=1.
如圖,一次函數y=x+1的圖象與反比例函數y=$\frac{k}{x}$(x>0)的圖象交于點M,作MN⊥x軸,N為垂足,且ON=1.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com