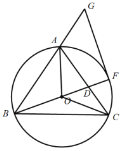
【題目】如圖，在
中，
，
是的外接圓，連結OA、OB、OC，延長BO與AC交于點D，與交于點F，延長BA到點G，使得
，連接FG.
備用圖
（1）求證：FG是的切線；
（2）若的半徑為4.
①當
，求AD的長度；
②當
是直角三角形時，求的面積.
【答案】（1）見解析；（2）①
，②當
時，
；當
時，
.
【解析】
（1）連接AF，由圓周角定理的推論可知
，根據等腰三角形的性質及圓周角定理的推論可證
，
，從而可得
，然后根據切線的判定方法解答即可；
（2）①連接CF，根據“SSS”證明
，由全等三角形及等腰三角形的性質可得
，進而可證
，由平行線分線段成比例定理可證
，可求
，然后由相交弦定理求解即可；
②分兩種情況求解即可，（i）當時，（ii）當時.
（1）連接AF，
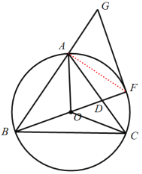
∵BF為
的直徑，
∴
，
，
∴，
∵
，∴
，
∵，，
∴
，
∴，即
.
又∵OF為半徑，
∴FG是的切線.
（2）①連接CF，
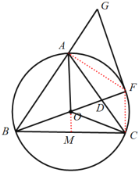
則
，
∵AB=AC，OB=OC，OA=OA，
∴，
∴，
∴，
∴
，
∴.
∵半徑是4，
，∴
，
，
∴
，即，
又由相交弦定理可得：
，
∴
，即
，
∴（舍負）；
（2）②∵
為直角三角形，不可能等于
.
∴（i）當時，則
，
由于
，∴
，
，
∴
，
∴
，
，
∴
；
（ii）當時，
∵
，∴
是等腰直角三角形，∴
，
延長AO交BC于點M，
∵AB=AC，
∴弧AB=弧AC，
∴
，
∴
，
∴
，
∴
.
科目：初中數學 來源： 題型：
【題目】圖 1、圖 2 均是 6×6 的正方形網格，每個小正方形的頂點稱為格點，小正方形的邊長為 1，點 A、B、C、D 均在格點上．在圖 1、圖 2 中，只用無刻度的直尺，在給定的網格中按要求畫圖，所畫圖形的頂點均在格點上，不要求寫出畫法．
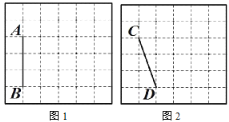
（1）在圖 1 中以線段 AB 為邊畫一個△ABM，使∠ABM=45°，且△ABM 的面積為 6；
（2）在圖 2 中以線段 CD 為邊畫一個四邊形 CDEF，使∠CDE＝∠CFE=90°，且四邊形 CDEF 的面積為 8．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，拋物線y＝mx2﹣4mx+n（m＞0）與x軸交于A、B兩點（點A在原點左側），與y軸交于點C，且OB＝2OA，連接AC、BC．
（1）求A、B兩點的坐標；
（2）將線段AC繞點A旋轉60°得到線段AC'，若點C'在拋物線的對稱軸上，求出此時拋物線的函數解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
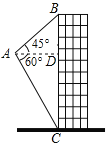
【題目】如圖，航拍無人機從A處測得一幢建筑物頂部B的仰角為45°，測得底部C的角為60°，此時航拍無人機與該建筑物的水平距離AD為80m，那么該建筑物的高度BC為_____m（結果保留根號）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了迎接體育中考，某校九（1）班的體育老師對全班45名學生進行了一次體育模擬測試(得分均為整數)，成績滿分為10分，該班的體育委員根據這次測試成績，制作了統計圖和分析表如下：
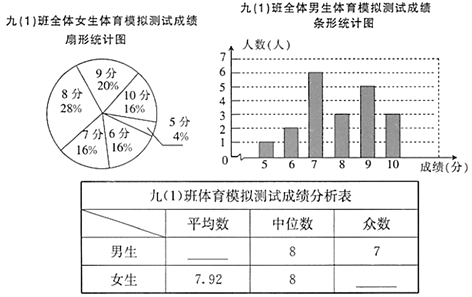
根據以上信息，解答下列問題．
（1）這個班共有男生_________人，女生有____________人．
（2）請你補全九(1)班體育模擬測試成績分析表．
（3）你認為在這次體育模擬測試中，九（1）班的全體男生和全體女生，誰的表現更好一些？請寫出一條支持你的看法的理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
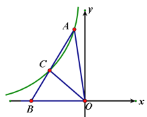
【題目】如圖，在△AOB中，OC平分∠AOB，
，反比例函數
圖像經過點A、C兩點，點B在x軸上，若△AOB的面積為7，則k的值為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】國家教育部為支援西部教育發展，計劃投入大量資金在西部各省修建A，B兩類大型圖書館共10個
若修建A類圖書館1個，B類圖書館2個，共需400萬元；若修建A類圖書館2個，B類圖書館1個，共需350萬元．
（1）求修建A類和B類圖書館每個各需多少萬元？
（2）預計在該計劃上A類和B類圖書館年均閱覽量分別為60萬人次和100萬人次若教育部投入A類和B類圖書館的總費用不超過1200萬元，且確保這10個圖書館的年均閱覽量總和不少于680萬人次．如果你是領導，從節約投資費用考慮，請設計出可行的方案．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
