
(本題滿分12分)如圖1,四邊形OABC中,OA=a,OC=3,BC=2,∠AOC=∠BCO=90°,經過點O的直線l將四邊形分成兩部分,直線l與OC所成的角設為θ,將四邊形OABC的直角∠OCB沿直線l折疊,點C落在點D處(如圖1).
(1)若折疊后點D恰為AB的中點(如圖2),求θ的度數;
(2)若θ=45°,四邊形OABC的直角∠OCB沿直線l折疊后,
①點B落在點四邊形OABC的邊AB上的E處(如圖3),求a的值;
②若點E落在四邊形OABC的外部,直接寫出a的取值范圍.

(1)30°;(2)① ,②
,②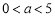 .
.
【解析】
試題分析:(1)延長ND交OA的延長線于M,根據折疊性質得∠CON=∠DON=θ,∠ODN=∠C=90°,由點D為AB的中點得到D點為MN的中點,所以OD垂直平分MN,則OM=ON,根據等腰三角形的性質得∠MOD=∠NOD=θ,則∠θ+∠θ+∠θ=90°,計算得到∠θ=30°;
(2)①作ED⊥OA于D,根據折疊性質得AB⊥直線l,OD=OC=3,DE=BC=2,由于θ=45°,AB⊥直線l,即直線l平分∠AOC,則∠A=45°,所以△ADE為等腰直角三角形,則AD=DE=2,所以OA=OD+AD=3+2=5,即a=5;
②若點E落在四邊形OABC的外部,則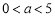 .
.
試題解析:(1)如圖2,延長ND交OA的延長線于M,
∵四邊形OABC的直角∠OCB沿直線l折疊,點C落在點D處,∴∠CON=∠DON=θ,∠ODN=∠C=90°,
∵點D為AB的中點,∴D點為MN的中點,∴OD垂直平分MN,∴OM=ON,
∴∠MOD=∠NOD=θ,∴∠θ+∠θ+∠θ=90°,∴∠θ=30°;故答案為30°;
(2)①如圖3,作ED⊥OA于D,
∵四邊形OABC的直角∠OCB沿直線l折疊后,點B落在點四邊形OABC的邊AB上的E處,
∴AB⊥直線l,OD=OC=3,DE=BC=2,
∵θ=45°,AB⊥直線l,即直線l平分∠AOC,∴∠A=45°,∴△ADE為等腰直角三角形,
∴AD=DE=2,∴OA=OD+AD=3+2=5,∴a=5;
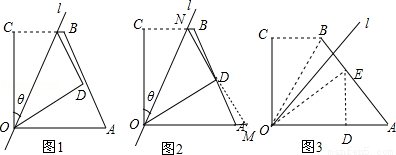
②若點E落在四邊形OABC的外部,則 .
.
考點:翻折變換(折疊問題).


科目:初中數學 來源:2014-2015學年江蘇省泰興市七年級上學期期中考試數學試卷(解析版) 題型:解答題
(本題8分)如圖,△ABC中,∠A=60°.

(1)求作一點P,使得點P到B、C兩點的距離相等,并且點P到AB、BC的距離也相等(尺規作圖,不寫作法,保留作圖痕跡);
(2)在(1)的條件下,若∠ACP=15°,求∠ABP的度數.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省附屬初級中學九年級上學期期中考試數學試卷(解析版) 題型:選擇題
已知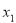 、
、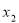 是一元二次方程
是一元二次方程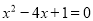 的兩個根,則
的兩個根,則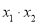 等于 ( )
等于 ( )
A.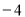 B.
B.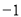 C.1 D.4
C.1 D.4
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省蘇州市高新區九年級上學期期中聯考數學試卷(解析版) 題型:填空題
如果函數 的圖象經過平面直角坐標系的四個象限,那么
的圖象經過平面直角坐標系的四個象限,那么 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com