
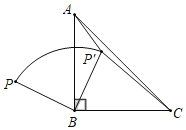
【題目】如圖,點P是等腰Rt△ABC外一點,把線段BP繞點B順時針旋轉90°得到線段BP',已知∠AP'B=135°,P'A:P'C=1:3,則P'A:PB=_____.
【答案】![]()
【解析】
連接AP和PP′,證明△ABP≌△CBP′,設P′A=x,則AP=3x,表示出BP,即可求出.
解:如圖,連接AP和PP′,
∵BP繞點B順時針旋轉90°到BP′,
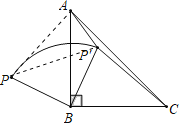
∴BP=BP′,∠ABP+∠ABP′=90°,
又∵△ABC是等腰直角三角形,
∴AB=BC,∠CBP′+∠ABP′=90°,
∴∠ABP=∠CBP′,
在△ABP和△CBP′中,
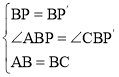 ,
,
∴△ABP≌△CBP′(SAS),
∴AP=P′C,
∵P′A:P′C=1:3,
∴AP=3P′A,
∵△PBP′是等腰直角三角形,
∴∠BP′P=45°,PP′=![]() PB,
PB,
∵∠AP′B=135°,
∴∠AP′P=135°﹣45°=90°,
∴△APP′是直角三角形,
設P′A=x,則AP=3x,
根據勾股定理,PP′=![]() =
=![]() =
=![]() ,
,
∴PP′=![]() PB=
PB=![]() ,
,
解得PB=2x,
∴P′A:PB=x:2x=1:2,
故答案為![]() .
.


科目:初中數學 來源: 題型:
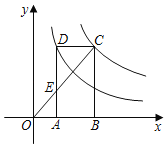
【題目】如圖,矩形ABCD的頂點C,D分別在反比例函數y=![]() (x>0).y=
(x>0).y=![]() (x>0)的圖象上,頂點A,B在x軸上,連接OC,交DA于點E,則
(x>0)的圖象上,頂點A,B在x軸上,連接OC,交DA于點E,則![]() =_____.
=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點C(O,4),與
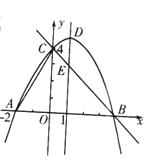
軸交于點C(O,4),與![]() 軸交于點A和點B,其中點A的坐標為(-2,0),拋物線的對稱軸
軸交于點A和點B,其中點A的坐標為(-2,0),拋物線的對稱軸![]() 與拋物線交于點D,與直線BC交于點E.
與拋物線交于點D,與直線BC交于點E.
(1)求拋物線的解析式;
(2)若點F是直線BC上方的拋物線上的一個動點,是否存在點F使四邊形ABFC的面積為17,若存在,求出點F的坐標;若不存在,請說明理由;
(3)平行于DE的一條動直線Z與直線BC相交于點P,與拋物線相交于點Q,若以D、E、P、Q為頂點的四邊形是平行四邊形,求點P的坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P是等邊三角形ABC內的一點,且PA=6,PB=8,PC=10.
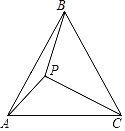
(1)尺規作圖:作出將△PAC繞點A逆時針旋轉60°后所得到的△P′AB(不要求寫作法,但需保留作圖痕跡).
(2)求點P與點P′之間的距離及∠APB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正面分別寫著數字1,2,3的三張卡片(注:這三張卡片的形狀、大小、質地,顏色等其他方面完全相同,若背面上放在桌面上,這三張卡片看上去無任何差別)洗勻后,背面向上放在桌面上,從中先隨機抽取一張卡片,記該卡片上的數字為x,再把剩下的兩張卡片洗勻后,背面向上放在桌面上,再從這兩張卡片中隨機抽取一張卡片,記該卡片上的數字為y.
(1)用列表法或樹狀圖法(樹狀圖也稱樹形圖)中的一種方法,寫出(x,y)所有可能出現的結果.
(2)求取出的兩張卡片上的數字之和為偶數的概率P.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,頂點為點
,頂點為點![]() .
.
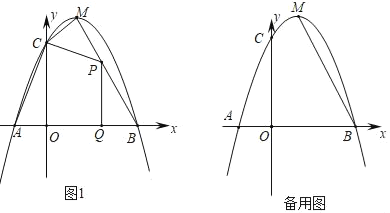
(1)求這條拋物線的解析式及直線![]() 的解析式;
的解析式;
(2)![]() 段
段![]() 上一動點(點
上一動點(點![]() 不與點
不與點![]() 、
、![]() 重合),過點
重合),過點![]() 向
向![]() 軸引垂線,垂足為
軸引垂線,垂足為![]() ,設
,設![]() 的長為
的長為![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() .求
.求![]() 與
與![]() 之間的函數關系式及自變量
之間的函數關系式及自變量![]() 的取值范圍;
的取值范圍;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 為等腰三角形?若存在,請直接寫出點
為等腰三角形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
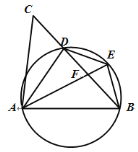
【題目】如圖,D是△ABC的BC邊上一點,連接AD,作△ABD的外接圓,將△ADC沿直線AD折疊,點C的對應點E落在圓上,連接AE,AE與BD相交于點F.
(1)求證:AE=AB;
(2)若E為弧BD的中點,試說明:DE2=EF·AE;
(3)在(2)的條件下,若cos∠ADB=![]() ,BE=2,求AF的長.
,BE=2,求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
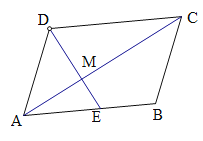
【題目】(操作、填空)如圖,![]() 中,對角線
中,對角線![]() ,點
,點![]() 是邊
是邊![]() 上一動點,連接
上一動點,連接![]() 交
交![]() 于點
于點![]() .
.
(1)若![]() ,則
,則![]() 的長為 ;(用含
的長為 ;(用含![]() 的式子表示,下同)
的式子表示,下同)
(2)若![]() ,則
,則![]() 的長為 ;
的長為 ;
(3)若![]() ,則
,則![]() 的長為 ;
的長為 ;
……
(猜想、論證)若![]() ,請用含
,請用含![]() ,
,![]() 的式子表示
的式子表示![]() ,并證明結論的正確性.
,并證明結論的正確性.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數圖象如圖所示,根據圖象可得:
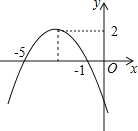
(1)拋物線頂點坐標_____.
(2)對稱軸為_____.
(3)當_____時,y隨著x得增大而增大
(4)當_____時,y>0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com