
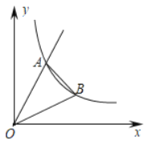
【題目】如圖,正比例函數y1=k1x的圖象與反比例函數y2=![]() (x>0)的圖象相交于點A(
(x>0)的圖象相交于點A(![]() ,2
,2![]() ),點B是反比例函數圖象上一點,它的橫坐標是3,連接OB,AB,則△AOB的面積是_____.
),點B是反比例函數圖象上一點,它的橫坐標是3,連接OB,AB,則△AOB的面積是_____.
【答案】2![]()
【解析】
把點A(![]() ,2
,2![]() )代入y1=k1x和y2=
)代入y1=k1x和y2=![]() (x>0)可求出k1、k2的值,即可正比例函數和求出反比例函數的解析式,過點B作BD∥x軸交OA于點D,結合點B的坐標即可得出點D的坐標,再根據三角形的面積公式即可求出△AOB的面積.
(x>0)可求出k1、k2的值,即可正比例函數和求出反比例函數的解析式,過點B作BD∥x軸交OA于點D,結合點B的坐標即可得出點D的坐標,再根據三角形的面積公式即可求出△AOB的面積.
∵正比例函數y1=k1x的圖象與反比例函數y2=![]() (x>0)的圖象相交于點A(
(x>0)的圖象相交于點A(![]() ,2
,2![]() ),
),
∴2![]() =
=![]() k1,2
k1,2![]() =
=![]() ,
,
∴k1=2,k2=6,
∴正比例函數為y=2x,反比例函數為:y=![]() ,
,
∵點B是反比例函數圖象上一點,它的橫坐標是3,
∴y=![]() =2,
=2,
∴B(3,2),
過點B作BD∥x軸交OA于點D,如圖
則D(1,2),
∴BD=3﹣1=2.
∴S△AOB=S△ABD+S△OBD=![]() ×2×(2
×2×(2![]() ﹣2)+
﹣2)+![]() ×2×2=2
×2×2=2![]() ,
,
故答案為2![]() .
.



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ),
),![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() .
.
(1)求該拋物線的解析式,并寫出它的對稱軸;
(2)點![]() 為拋物線對稱軸上一點,連接
為拋物線對稱軸上一點,連接![]() ,若
,若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)已知![]() ,若
,若![]() 是拋物線上一個動點(其中
是拋物線上一個動點(其中![]() ),連接
),連接![]() ,求
,求![]() 面積的最大值及此時點
面積的最大值及此時點![]() 的坐標.
的坐標.
(4)若點![]() 為拋物線對稱軸上一點,拋物線上是否存在點
為拋物線對稱軸上一點,拋物線上是否存在點![]() ,使得以
,使得以![]() 為頂點的四邊形是平行四邊形?若存在,請直接寫出所有滿足條件的點
為頂點的四邊形是平行四邊形?若存在,請直接寫出所有滿足條件的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD的對角線相交于點O,且點O是BD的中點,若AB=AD=5,BD=8,∠ABD=∠CDB,則四邊形ABCD的面積為( )

A.40B.24C.20D.15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一塊斜邊長30cm的直角三角形木板(Rt△ACB)上截取一個正方形CDEF,點D在邊BC上,點E在斜邊AB上,點F在邊AC上,若AF:AC=1:3,則這塊木板截取正方形CDEF后,剩余部分的面積為( )
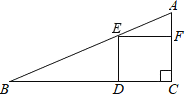
A. 100cm2B. 150cm2C. 170cm2D. 200cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“勤勞”是中華民族的傳統美德,學校要求同學們在家里幫助父母做一些力所能及的家務.在本學期開學初,小穎同學隨機調查了部分同學寒假在家做家務的總時間,設被調查的每位同學寒假在家做家務的總時間為x小時,將做家務的總時間分為五個類別:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并將調查結果制成如下兩幅不完整的統計圖:
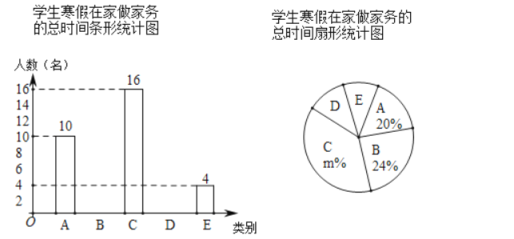
根據統計圖提供的信息,解答下列問題:
(1)本次共調查了 名學生;
(2)請根據以上信息直接在答題卡中補全條形統計圖;
(3)扇形統計圖中m的值是 ,類別D所對應的扇形圓心角的度數是 度;
(4)若該校有800名學生,根據抽樣調查的結果,請你估計該校有多少名學生寒假在家做家務的總時間不低于20小時.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級(1)班全班50名同學組成五個不同的興趣愛好小組,每人都參加且只能參加一個小組,統計(不完全)人數如下表:
編號 | 一 | 二 | 三 | 四 | 五 |
人數 |
| 15 | 20 | 10 |
|
已知前面兩個小組的人數之比是![]() .
.
解答下列問題:
(1)![]() .
.
(2)補全條形統計圖:
(3)若從第一組和第五組中任選兩名同學,求這兩名同學是同一組的概率.(用樹狀圖或列表把所有可能都列出來)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場以每件280元的價格購進一批商品,當每件商品售價為360元時,每月可售出60件,為了迎接“雙11”節,擴大銷售,商場決定采取適當降價的方式促銷,經調查發現,如果每件商品降價1元,那么商場每月就可以多售出5件. 設每件降價x元:
(1)降價后每件利潤 元,商場能售出 件.
(2)要使商場每月銷售這種商品的利潤達到7200元,且更有利于減少庫存,則每件商品應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現今“微信運動”被越來越多的人關注和喜愛,某興趣小組隨機調查了我市50名教師某日“微信運動”中的步數情況進行統計整理,繪制了如下的統計圖表(不完整):
步數 | 頻數 | 頻率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
請根據以上信息,解答下列問題:
(1)寫出a,b,c,d的值并補全頻數分布直方圖;
(2)本市約有37800名教師,用調查的樣本數據估計日行走步數超過12000步(包含12000步)的教師有多少名?
(3)若在50名被調查的教師中,選取日行走步數超過16000步(包含16000步的兩名教師與大家分享心得,求被選取的兩名教師恰好都在20000步(包含20000步)以上的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】襄陽市某農谷生態園響應國家發展有機農業政策,大力種植有機蔬菜.某超市看好甲、乙兩種有機蔬菜的市場價值,經調查,這兩種蔬菜的進價和售價如下表所示:
有機蔬菜種類 | 進價(元/ | 售價(元/ |
甲 |
| 16 |
乙 |
| 18 |
(1)該超市購進甲種蔬菜10![]() 和乙種蔬菜5
和乙種蔬菜5![]() 需要170元;購進甲種蔬菜6
需要170元;購進甲種蔬菜6![]() 和乙種蔬菜10
和乙種蔬菜10![]() 需要200元.求
需要200元.求![]() ,
,![]() 的值;
的值;
(2)該超市決定每天購進甲、乙兩種蔬菜共100![]() 進行銷售,其中甲種蔬菜的數量不少于20
進行銷售,其中甲種蔬菜的數量不少于20![]() ,且不大于70
,且不大于70![]() .實際銷售時,由于多種因素的影響,甲種蔬菜超過60
.實際銷售時,由于多種因素的影響,甲種蔬菜超過60![]() 的部分,當天需要打5折才能售完,乙種蔬菜能按售價賣完.求超市當天售完這兩種蔬菜獲得的利潤額
的部分,當天需要打5折才能售完,乙種蔬菜能按售價賣完.求超市當天售完這兩種蔬菜獲得的利潤額![]() (元)與購進甲種蔬菜的數量
(元)與購進甲種蔬菜的數量![]() (
(![]() )之間的函數關系式,并寫出
)之間的函數關系式,并寫出![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,超市在獲得的利潤額![]() (元)取得最大值時,決定售出的甲種蔬菜每千克捐出
(元)取得最大值時,決定售出的甲種蔬菜每千克捐出![]() 元,乙種蔬菜每千克捐出
元,乙種蔬菜每千克捐出![]() 元給當地福利院,若要保證捐款后的盈利率不低于20%,求
元給當地福利院,若要保證捐款后的盈利率不低于20%,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com