
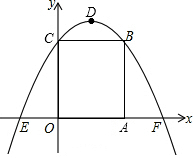
 如圖,在平面直角坐標系中,矩形OABC的頂點A、C的坐標分別為(2,0)、(0,3),拋物線y=-x2+bx+c經過B、C兩點,交x軸于點E和點F,動點P從點E出發,以每秒1個單位的速度沿E→O→C→B向點B運動,動點Q從點B出發,以相同的速度沿B→A→F運動,到點F后,繼續沿x軸正方向運動,當點P到達點B時點Q隨之停止運動.
如圖,在平面直角坐標系中,矩形OABC的頂點A、C的坐標分別為(2,0)、(0,3),拋物線y=-x2+bx+c經過B、C兩點,交x軸于點E和點F,動點P從點E出發,以每秒1個單位的速度沿E→O→C→B向點B運動,動點Q從點B出發,以相同的速度沿B→A→F運動,到點F后,繼續沿x軸正方向運動,當點P到達點B時點Q隨之停止運動.分析 (1)利用待定系數法即可解決問題.
(2)分四種情形討論①如圖當點P在OE上時,矩形的對角線AC與OB交于點H,則H(1,$\frac{3}{2}$).求出直線PQ的解析式(用t表示),然后利用待定系數法解決.②當點P在線段OC上,點Q在線段AB上時,直線PQ不可能經過點H,此時不存在.③當點P在線段OC上,點Q在射線AF上時,方法類似①,④當點P在線段BC上時,顯然直線PQ不經過點H,此時不存在.
(3)分兩種情形①如圖3中,當DP=QD時,△DPQ是等腰三角形.②如圖3中,當PD=PQ時,△PQD是等腰三角形.分別列出方程即可解決.
(4)分兩種情形①如圖4中,當點Q與點A重合時,OP=OA,易知四邊形PCFQ是等腰梯形,是軸對稱圖形,②如圖5中,當點Q在線段BC上時,易知四邊形CPQF是平行四邊形,是中心對稱圖形,即可解決問題.
解答 解:(1)∵拋物線拋y=-x2+bx+c經過B、C兩點經過C(0,3),B(2,3),
∴$\left\{\begin{array}{l}{c=3}\\{-4+2b+c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴拋物線的解析式為y=-x2+2x+3,
(2)①如圖當點P在OE上時,矩形的對角線AC與OB交于點H,則H(1,$\frac{3}{2}$).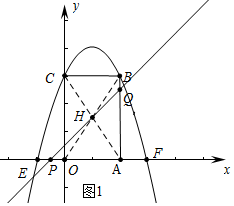
∵P(t-1,0),Q(2,3-t),
∴直線PQ的解析式為y=x+1-t,
當直線PQ經過點H時,直線PQ平分矩形ABCD的面積,
∴$\frac{3}{2}$=1+1-t,
∴t=$\frac{1}{2}$.
②當點P在線段OC上,點Q在線段AB上時,直線PQ不可能經過點H,此時不存在.
③當點P在線段OC上,點Q在射線AF上時,
∵P(0,t-1),Q(2+t-3,0),
∴直線PQ的解析式為y=-x+t-1,
當直線PQ經過點H時,直線PQ平分矩形ABCD的面積,
∴$\frac{3}{2}$=-1+t-1,
∴t=$\frac{7}{2}$,
④當點P在線段BC上時,顯然直線PQ不經過點H,此時不存在.
綜上所述,當t=$\frac{1}{2}$s或$\frac{7}{2}$s時,直線PQ平分矩形ABCD的面積.
(3)①如圖3中,當DP=QD時,△DPQ是等腰三角形.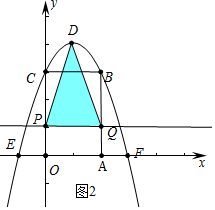
根據對稱性可知,PC=BQ,
∴4-t=t,
∴t=2.
②如圖3中,當PD=PQ時,△PQD是等腰三角形.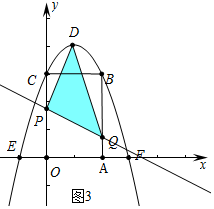
∵D(1,4),P(0,t-1),Q(2,3-t),
∴12+(t-5)2=22+(4-t+3-t)2,
∴t=3.
綜上所述,t=2或3時,△DPQ是等腰三角形.
(4)①如圖4中,當點Q與點A重合時,OP=OA,易知四邊形PCFQ是等腰梯形,是軸對稱圖形,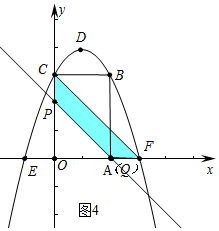
當點Q在射線AF上時,OP=OQ=t-1,四邊形PCFQ是等腰梯形,
∴3≤t≤4時,四邊形PCQF是軸對稱圖形.
②如圖5中,當點Q在線段BC上時,易知四邊形CPQF是平行四邊形,是中心對稱圖形,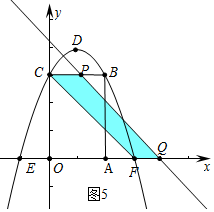
∴4<t≤6時,四邊形CPQF是中心對稱圖形.
綜上所述,3≤t≤6時,以P、Q、C、F為頂點的四邊形為軸對稱圖形或中心對稱圖形.
點評 本題考查二次函數綜合題、一次函數的應用、矩形的性質、等腰三角形的判定和性質,軸對稱圖形、中心對稱圖形的性質等知識,解題的關鍵是靈活運用所學知識,學會用分類討論的思想思考問題,學會利用圖象解決問題,體現了數形結合的思想,屬于中考壓軸題.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:初中數學 來源: 題型:解答題
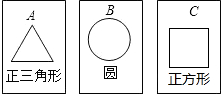 如圖,有三張背面完全相同的紙牌A、B、C,其中正面分別畫有三種不同的幾何圖形,小華將這3張紙牌背面朝上洗勻后摸出一張,放回洗勻后再摸出一張,請你用畫樹狀圖或列表的方法,求摸出的兩張紙牌面上所畫幾何圖形既是軸對稱圖形又是中心對稱圖形的概率.
如圖,有三張背面完全相同的紙牌A、B、C,其中正面分別畫有三種不同的幾何圖形,小華將這3張紙牌背面朝上洗勻后摸出一張,放回洗勻后再摸出一張,請你用畫樹狀圖或列表的方法,求摸出的兩張紙牌面上所畫幾何圖形既是軸對稱圖形又是中心對稱圖形的概率.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 兩個銳角的和一定是鈍角 | |
| B. | 兩條平行線被第三條直線所截,同旁內角的平分線互相垂直 | |
| C. | 兩條直線被第三條直線所截,同旁內角互補 | |
| D. | 直線外一點到這條直線的垂線段,叫做這點到該直線的距離 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 當x<2,y隨x的增大而減小 | B. | 函數的對稱軸是直線x=1 | ||
| C. | 函數的開口方向向上 | D. | 函數圖象與y軸的交點坐標是(0,-3) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

| 平均成績(分) | 中位數(分) | 眾數(分) | 方差(S2) | |
| A同學 | 80 | 80 | 80 | 60 |
| B同學 | 80 | 85 | 90 | 260 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com