
【題目】如圖,在![]() 中,
中,![]() 為
為![]() 邊上的中點.
邊上的中點.
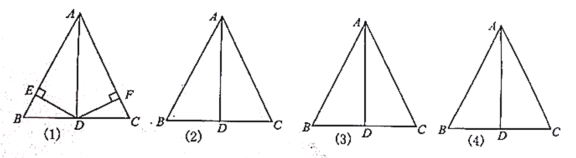
(1)若![]() 于
于![]() ,
,![]() 于
于![]() ,連接
,連接![]() .判斷
.判斷![]() 的形狀,并證明;
的形狀,并證明;
(2)若![]() 分別是
分別是![]() 上的中線,連接
上的中線,連接![]() .判斷
.判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)若![]() 分別是
分別是![]() 的平分線,連接
的平分線,連接![]() .判斷
.判斷![]() 的關(guān)系,不需證明;
的關(guān)系,不需證明;
(4)若分別在![]() 上任取一點
上任取一點![]() ,且
,且![]() ,連接
,連接![]() .在不添加輔助線的情況下,你還能得到哪些不同于上面的正確結(jié)論?請寫出至少四條,不需證明.
.在不添加輔助線的情況下,你還能得到哪些不同于上面的正確結(jié)論?請寫出至少四條,不需證明.
【答案】(1)![]() 是等腰三角形,理由見解析;(2)
是等腰三角形,理由見解析;(2)![]() 是等腰三角形,理由見解析;(3)
是等腰三角形,理由見解析;(3)![]() 且
且![]() ;(4)
;(4)![]() 是等腰三角形,
是等腰三角形,![]() 是EF的垂直平分線,
是EF的垂直平分線,![]() ,
,![]() .
.
【解析】
(1)依據(jù)等腰三角形三線合一的性質(zhì),及角平分線的性質(zhì),可以證明![]() 是等腰三角形;
是等腰三角形;
(2)由![]() 分別是
分別是![]() 上的中線,
上的中線,![]() ,得
,得![]() ,依據(jù)SAS證明
,依據(jù)SAS證明![]() ≌
≌![]() ,從而
,從而![]() ,即證明
,即證明![]() 是等腰三角形;
是等腰三角形;
(3)![]() 分別是
分別是![]() 的平分線,結(jié)合三線合一中AD是高,可得
的平分線,結(jié)合三線合一中AD是高,可得![]() ,從而
,從而![]() 即
即![]() ,
,![]() ≌
≌![]() (ASA),依據(jù)全等的性質(zhì)得
(ASA),依據(jù)全等的性質(zhì)得![]() ,所以
,所以![]() 且
且![]() ;
;
(4)依據(jù)軸對稱的知識即可作答.
(1)![]() 是等腰三角形,理由如下:
是等腰三角形,理由如下:

∵在![]() 中,
中,![]() 為
為![]() 邊上的中點,
邊上的中點,
∴![]() 是平分
是平分![]() ,
,
又∵![]() ,
,![]() ,
,
![]() ,
,
∴![]() 是等腰三角形;
是等腰三角形;
(2)![]() 是等腰三角形,理由如下:
是等腰三角形,理由如下:

∵![]() 分別是
分別是![]() 上的中線,
上的中線,![]()
∴![]() ,
,
又∵由![]() 是平分
是平分![]() 得
得![]() ,
,
![]() ,
,
∴![]() ≌
≌![]() (SAS),
(SAS),
∴![]() ,
,
∴![]() 是等腰三角形;
是等腰三角形;
(3)![]() .
.

(4)![]() 是等腰三角形,
是等腰三角形,![]() 是EF的垂直平分線,
是EF的垂直平分線,![]() ,
,![]() .(答案不唯一,依據(jù)軸對稱回答即可).
.(答案不唯一,依據(jù)軸對稱回答即可).


科目:初中數(shù)學(xué) 來源: 題型:
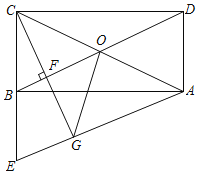
【題目】如圖,在矩形ABCD中,AC、BD相交于點O,過點A作BD的平行線AE交CB的延長線于點E.
(1)求證:BE=BC;
(2)過點C作CF⊥BD于點F,并延長CF交AE于點G,連接OG.若BF=3,CF=6,求四邊形BOGE的周長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
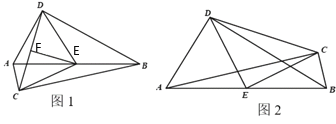
【題目】已知:如圖,Rt△ABC和Rt△ABD中,∠ACB=∠ADB=90°,E為AB中點.
(1)若兩個直角三角形的直角頂點在AB的異側(cè)(如圖1),連接CD,取CD中點F,連接EF、DE、CE,則DE與CE數(shù)量關(guān)系為 ,EF與CD位置關(guān)系為 ;
(2)若兩個直角三角形的直角頂點在AB的同側(cè)(如圖2),連接CD、DE、CE.
①若∠CAB=25°,∠DBA=35°,判斷△DEC的形狀,并說明理由;
②若∠CAB+∠DBA=![]() ,當(dāng)
,當(dāng)![]() 為多少度時,△DEC為等腰直角三角形,并說明理由.
為多少度時,△DEC為等腰直角三角形,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某童裝店在服裝銷售中發(fā)現(xiàn):進貨價每件60元,銷售價每件100元的某童裝每天可售出20件![]() 為了迎接“六一兒童節(jié)”,童裝店決定采取適當(dāng)?shù)拇黉N措施,擴大銷售量,增加盈利
為了迎接“六一兒童節(jié)”,童裝店決定采取適當(dāng)?shù)拇黉N措施,擴大銷售量,增加盈利![]() 經(jīng)調(diào)查發(fā)現(xiàn):如果每件童裝降價1元,那么每天就可多售出2件.
經(jīng)調(diào)查發(fā)現(xiàn):如果每件童裝降價1元,那么每天就可多售出2件.
![]() 如果童裝店想每天銷售這種童裝盈利1050元,同時又要使顧客得到更多的實惠,那么每件童裝應(yīng)降價多少元?
如果童裝店想每天銷售這種童裝盈利1050元,同時又要使顧客得到更多的實惠,那么每件童裝應(yīng)降價多少元?
![]() 每件童裝降價多少元時,童裝店每天可獲得最大利潤?最大利潤是多少元?
每件童裝降價多少元時,童裝店每天可獲得最大利潤?最大利潤是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角坐標(biāo)系中,矩形![]() 的頂點
的頂點![]() 與坐標(biāo)原點重合,頂點
與坐標(biāo)原點重合,頂點![]() 、
、![]() 分別在坐標(biāo)軸上,頂點
分別在坐標(biāo)軸上,頂點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點.
的中點.
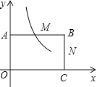
(1)若反比例函數(shù)![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() ,求該反比例函數(shù)的解析式,并通過計算判斷點
,求該反比例函數(shù)的解析式,并通過計算判斷點![]() 是否在該函數(shù)的圖象上;
是否在該函數(shù)的圖象上;
(2)若反比例函數(shù)![]() 的圖象與
的圖象與![]() (包括邊界)有公共點,請直接寫出
(包括邊界)有公共點,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖(1),在平行四邊形ABCD中,DE⊥AB,BF⊥CD,垂足分別為E、F,求證:AE=CF;
(2)如圖(2),在平行四邊形ABCD中,AC、BD是兩條對角線,求證AC2+BD2=2(AB2+BC2)
(3)如圖(3),PQ是△PMN的中線,若PM=11,PN=13,MN=10,求出PQ的長度.
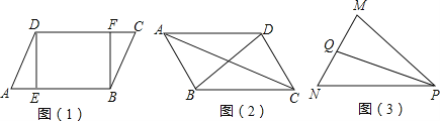
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,等邊![]() 中,
中,![]() ,
,![]() 關(guān)于
關(guān)于![]() 軸對稱,
軸對稱,![]() 交
交![]() 軸負半軸于點
軸負半軸于點![]() ,
,![]() .
.
(1)如圖1,求![]() 點坐標(biāo);
點坐標(biāo);
(2)如圖2,![]() 為
為![]() 軸負半軸上任一點,以
軸負半軸上任一點,以![]() 為邊作等邊
為邊作等邊![]() ,
,![]() 的延長線交
的延長線交![]() 軸于點
軸于點![]() ,求
,求![]() 的長;
的長;
(3)如圖3,在(1)的條件下,以![]() 為頂點作
為頂點作![]() 的角,它的兩邊分別與
的角,它的兩邊分別與![]() 、
、![]() 交于點
交于點![]() 和
和![]() ,連接
,連接![]() .探究線段
.探究線段![]() 、
、![]() 、
、![]() 之間的關(guān)系,并子以證明.
之間的關(guān)系,并子以證明.
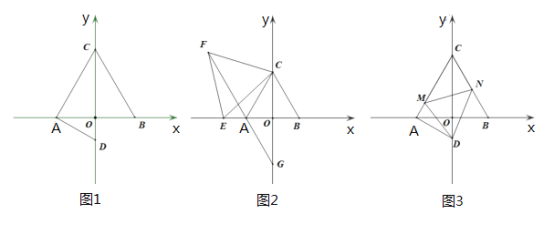
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線的頂點坐標(biāo)為![]() ,且經(jīng)過點
,且經(jīng)過點![]() ,與
,與![]() 軸交于
軸交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側(cè)),與
左側(cè)),與![]() 軸交于點
軸交于點![]() .
.
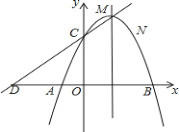
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 若直線
若直線![]() 經(jīng)過
經(jīng)過![]() 、
、![]() 兩點,且與
兩點,且與![]() 軸交于點
軸交于點![]() ,試證明四邊形
,試證明四邊形![]() 是平行四邊形;
是平行四邊形;
![]() 點
點![]() 在拋物線的對稱軸
在拋物線的對稱軸![]() 上運動,請?zhí)剿鳎涸?/span>
上運動,請?zhí)剿鳎涸?/span>![]() 軸上方是否存在這樣的
軸上方是否存在這樣的![]() 點,使以
點,使以![]() 為圓心的圓經(jīng)過
為圓心的圓經(jīng)過![]() 、
、![]() 兩點,并且與直線
兩點,并且與直線![]() 相切?若存在,請求出點
相切?若存在,請求出點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com