
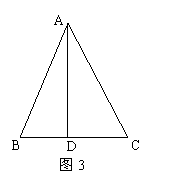
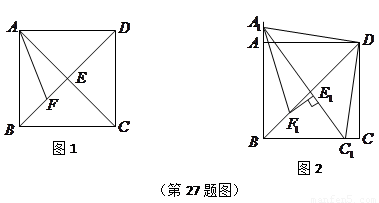
如圖1,在正方形![]() 中,
中,![]() 是
是![]() 上一點,
上一點,![]() 是
是![]() 延長線上一點,且
延長線上一點,且![]() .
.
(1)求證:![]() ;
;
(2)在圖1中,若![]() 在
在![]() 上,且
上,且![]() ,則
,則![]() 成立嗎?為什么?
成立嗎?為什么?
(3)根據你所學的知識,運用(1)、(2)解答中積累的經驗,完成下列各題:
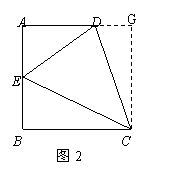
①如圖2,在直角梯形ABCD中,![]() ∥
∥![]()
![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,且∠DCE=45°,求DE的長;
的中點,且∠DCE=45°,求DE的長;
②如圖3,在△ABC中,∠BAC=45°,AD⊥BC,![]() ,則
,則
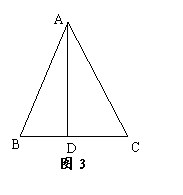

![]() 的面積為 (直接寫出結果,不需要寫出計算過程).
的面積為 (直接寫出結果,不需要寫出計算過程).
 |
證明:(1)在正方形ABCD中
 CB=CD, ∠B=∠CDA=90°
CB=CD, ∠B=∠CDA=90°
∴∠CDF=∠B =90°
∵DF=BE
∴△BCE≌△DCF(SAS)
∴CE=CF
(2)GE=BE+GD成立
理由:∵∠BCD=90°∠GCE=45°
∴∠BCE+∠GCD=45°
∵△BCE≌△DCF(已證)
∴∠BCE=∠DCF
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=45°
 ∴∠ECG=∠FCG=45°
∴∠ECG=∠FCG=45°
∵CE=CF ,CG=CG
∴△ECG≌△FCG(SAS)
∴GE=FG
∵FG=GD+DF
∴GE=BE+GD
 (3)①
(3)①
解:過點C作CG⊥AD交AD的延長線于點G,
由(1)和題設知 DE=DG+BE.
設DG=x,則AD=12-x,DE=x+6,
在Rt△ADE中,AD2+AE2=DE2
∴ 62+(12-x)2=(x+6)2 解得 x=4.
∴DE=6+4=10.
② 15.


科目:初中數學 來源: 題型:
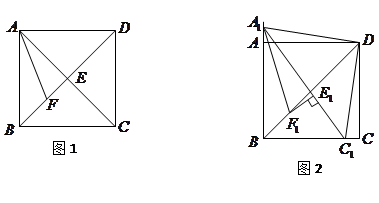
如圖1,在正方形![]() 中,對角線
中,對角線![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
(2)點![]() 從點
從點![]() 出發,沿著線段
出發,沿著線段![]() 向點
向點![]() 運動(不與點
運動(不與點![]() 重合),同時點
重合),同時點![]() 從點
從點![]() 出發,沿著
出發,沿著![]() 的延長線運動,點
的延長線運動,點![]() 與
與![]() 的運動速度相同,當動點
的運動速度相同,當動點![]() 停止運動時,另一動點
停止運動時,另一動點![]() 也隨之停止運動.如圖2,
也隨之停止運動.如圖2,![]() 平分
平分![]() ,交
,交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() ,請猜想
,請猜想![]() ,
,![]() 與
與![]() 三者之間的數量關系,并證明你的猜想;
三者之間的數量關系,并證明你的猜想;
(3)在(2)的條件下,當![]() ,
,![]() 時,求
時,求![]() 的長
的長
查看答案和解析>>
科目:初中數學 來源:2012屆山東省章丘市六中片區九年級學業水平考試數學卷 題型:解答題
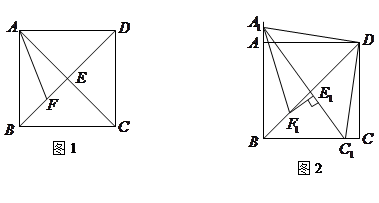
如圖1,在正方形 中,對角線
中,對角線 與
與 相交于點
相交于點 ,
,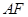 平分
平分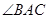 ,交
,交 于點
于點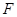 .
.
(1)求證: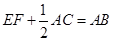 ;
;
(2)點 從點
從點 出發,沿著線段
出發,沿著線段 向點
向點 運動(不與點
運動(不與點 重合),同時點
重合),同時點 從點
從點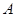 出發,沿著
出發,沿著 的延長線運動,點
的延長線運動,點 與
與 的運動速度相同,當動點
的運動速度相同,當動點 停止運動時,另一動點
停止運動時,另一動點 也隨之停止運動.如圖2,
也隨之停止運動.如圖2,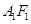 平分
平分 ,交
,交 于點
于點 ,過點
,過點 作
作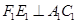 ,垂足為
,垂足為 ,請猜想
,請猜想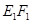 ,
,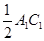 與
與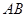 三者之間的數量關系,并證明你的猜想;
三者之間的數量關系,并證明你的猜想;
(3)在(2)的條件下,當 ,
,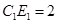 時,求
時,求 的長
的長
查看答案和解析>>
科目:初中數學 來源:2011—2012學年廣東省江門市第三中學八年級下學期期末模擬考試數學試卷 題型:解答題
如圖1,在正方形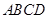 中,點
中,點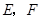 分別為邊
分別為邊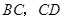 的中點,
的中點,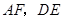 相交于點
相交于點 ,則可得結論:①
,則可得結論:①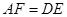 ;②
;②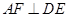 .(不需要證明)
.(不需要證明)
(1)如圖2,若點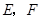 不是正方形
不是正方形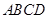 的邊
的邊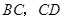 的中點,但滿足
的中點,但滿足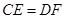 ,則上面的結論①,②是否仍然成立?(請直接回答“成立”或“不成立”)
,則上面的結論①,②是否仍然成立?(請直接回答“成立”或“不成立”)
(2)如圖3,若點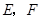 分別在正方形
分別在正方形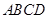 的邊
的邊 的延長線和
的延長線和 的延長線上,且
的延長線上,且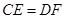 ,此時上面的結論1,2是否仍然成立?若成立,請寫出證明過程,若不成立,請說明理由.
,此時上面的結論1,2是否仍然成立?若成立,請寫出證明過程,若不成立,請說明理由.
(3)如圖4,在(2)的基礎上,連接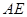 和
和 ,若點
,若點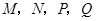 分別為
分別為 的中點,請判斷四邊形
的中點,請判斷四邊形 是“矩形、菱形、正方形、等腰梯形”中的哪一種?并寫出證明過程.
是“矩形、菱形、正方形、等腰梯形”中的哪一種?并寫出證明過程.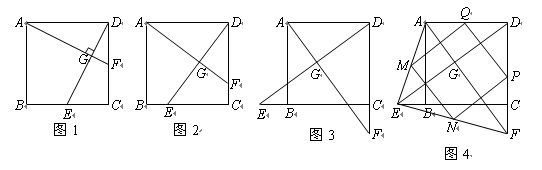
查看答案和解析>>
科目:初中數學 來源:2011-2012學年山東省章丘市片區六中九年級學業水平考試數學卷(解析版) 題型:解答題
如圖1,在正方形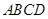 中,對角線
中,對角線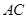 與
與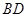 相交于點
相交于點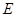 ,
,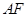 平分
平分 ,交
,交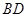 于點
于點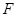 .
.
1.求證: ;
;
2.點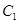 從點
從點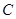 出發,沿著線段
出發,沿著線段 向點
向點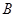 運動(不與點
運動(不與點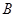 重合),同時點
重合),同時點 從點
從點 出發,沿著
出發,沿著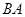 的延長線運動,點
的延長線運動,點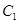 與
與 的運動速度相同,當動點
的運動速度相同,當動點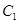 停止運動時,另一動點
停止運動時,另一動點 也隨之停止運動.如圖2,
也隨之停止運動.如圖2,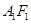 平分
平分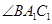 ,交
,交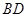 于點
于點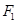 ,過點
,過點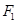 作
作 ,垂足為
,垂足為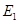 ,請猜想
,請猜想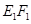 ,
,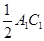 與
與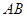 三者之間的數量關系,并證明你的猜想;
三者之間的數量關系,并證明你的猜想;
3.在(2)的條件下,當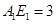 ,
, 時,求
時,求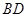 的長.
的長.
查看答案和解析>>
科目:初中數學 來源:2011-2012學年山東省章丘市片區九年級學業水平考試數學卷 題型:解答題
如圖1,在正方形 中,對角線
中,對角線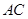 與
與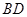 相交于點
相交于點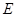 ,
, 平分
平分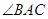 ,交
,交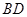 于點
于點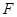 .
.
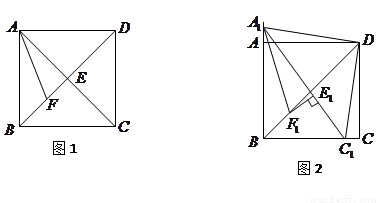
(1)求證: ;
;
(2)點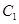 從點
從點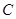 出發,沿著線段
出發,沿著線段 向點
向點 運動(不與點
運動(不與點 重合),同時點
重合),同時點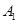 從點
從點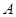 出發,沿著
出發,沿著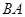 的延長線運動,點
的延長線運動,點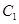 與
與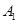 的運動速度相同,當動點
的運動速度相同,當動點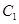 停止運動時,另一動點
停止運動時,另一動點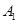 也隨之停止運動.如圖2,
也隨之停止運動.如圖2,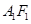 平分
平分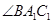 ,交
,交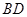 于點
于點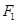 ,過點
,過點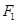 作
作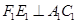 ,垂足為
,垂足為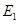 ,請猜想
,請猜想 ,
,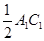 與
與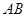 三者之間的數量關系,并證明你的猜想;
三者之間的數量關系,并證明你的猜想;
(3)在(2)的條件下,當 ,
, 時,求
時,求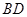 的長
的長
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com