
【題目】如圖,利用一面墻(墻的長度不超過45m),用80m長的籬笆圍一個矩形場地.

(1)怎樣圍才能使矩形場地的面積為750m2?
(2)能否使所圍矩形場地的面積為810m2,為什么?
(3)怎樣圍才能使圍出的矩形場地面積最大?最大面積為多少?請通過計算說明.
【答案】(1)當所圍矩形的長為30m、寬為25m時,能使矩形的面積為750m2;(2)不能使所圍矩形場地的面積為810m2;理由見解析;(3)當所圍矩形的長為40m、寬為20m時,能使矩形的面積最大,最大面積為800 m2.
【解析】
(1)設所圍矩形ABCD的長AB為x米,則寬AD為 ![]() (80x)米,根據矩形的面積公式建立方程求出解即可;
(80x)米,根據矩形的面積公式建立方程求出解即可;
(2)根據矩形的面積公式建立方程,根據根的判別式得出方程無實數解,從而得出結論;
(3)設矩形的面積為S,由矩形的面積公式可以得出S與x的關系,由關系式的性質就可以得出結論.
(1)設所圍矩形ABCD的長AB為x米,則寬AD為 ![]() (80﹣x)米,
(80﹣x)米,
由題意,得x![]() (80﹣x)=750,
(80﹣x)=750,
解得:x1=50,x2=30,
∵墻的長度不超過45m,
∴x=30,
∴![]() (80﹣x)=25,
(80﹣x)=25,
答:當所圍矩形的長為30m、寬為25m時,能使矩形場地的面積為750m2;
(2)不能.
理由:由x![]() (80﹣x)=810,整理得:x2﹣80x+1620=0.
(80﹣x)=810,整理得:x2﹣80x+1620=0.
∵△=b2﹣4ac=(﹣80)2﹣4×1×1620=﹣80<0,
∴方程沒有實數根.
因此不能使所圍矩形場地的面積為810m2;
(3)設矩形的面積為S,所圍矩形ABCD的長AB為x米,
由題意,得S=x![]() (80﹣x)=﹣
(80﹣x)=﹣![]() (x﹣40)2+800,
(x﹣40)2+800,
∴當x=40時,S最大=800,且符合題意,
∴![]() (80﹣x)=20,
(80﹣x)=20,
答:當所圍矩形的長為40m、寬為20m時,能使矩形的面積最大,最大面積為800 m2.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
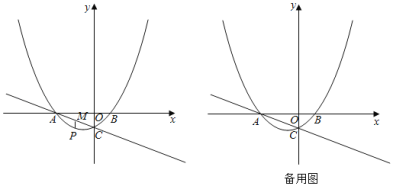
【題目】如圖,拋物線![]() 交x軸于A,B兩點,交y軸于點C.直線
交x軸于A,B兩點,交y軸于點C.直線![]() 經過點A,C.
經過點A,C.
(1)求拋物線的解析式;
(2)點P是拋物線上一動點,過點P作x軸的垂線,交直線AC于點M,設點P的橫坐標為m.
①當![]() 是直角三角形時,求點P的坐標;
是直角三角形時,求點P的坐標;
②作點B關于點C的對稱點![]() ,則平面內存在直線l,使點M,B,
,則平面內存在直線l,使點M,B,![]() 到該直線的距離都相等.當點P在y軸右側的拋物線上,且與點B不重合時,請直接寫出直線
到該直線的距離都相等.當點P在y軸右側的拋物線上,且與點B不重合時,請直接寫出直線![]() 的解析式.(k,b可用含m的式子表示)
的解析式.(k,b可用含m的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=kx+b和反比例函數y=![]() 圖象相交于A(2,4),B(n,﹣2)兩點.
圖象相交于A(2,4),B(n,﹣2)兩點.
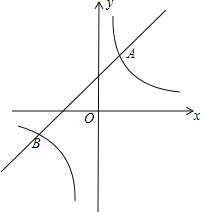
(1)求一次函數和反比例函數的解析式;
(2)觀察圖象,直接寫出不等式kx+b﹣![]() <0的解集;
<0的解集;
(3)點C(a,b),D(a,c)(a>2)分別在一次函數和反比例函數圖象上,且滿足CD=2,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=mx2﹣4mx+2m+1與x軸交于A(x1,0),B(x2,0)兩點,與y軸交于點C,且x2﹣x1=2.
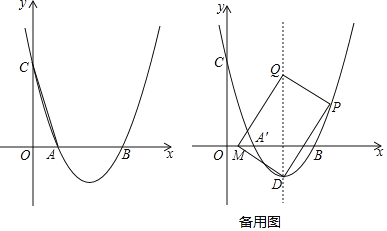
(1)求拋物線的解析式;
(2)E是拋物線上一點,∠EAB=2∠OCA,求點E的坐標;
(3)設拋物線的頂點為D,動點P從點B出發,沿拋物線向上運動,連接PD,過點P做PQ⊥PD,交拋物線的對稱軸于點Q,以QD為對角線作矩形PQMD,當點P運動至點(5,t)時,求線段DM掃過的圖形面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩校分別有一男一女共4名教師報名到農村中學支教.
(1)若從甲、乙兩校報名的教師中分別隨機選1名,則所選的2名教師性別相同的概率是 .
(2)若從報名的4名教師中隨機選2名,用列表或畫樹狀圖的方法求出這2名教師來自同一所學校的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C,D是⊙O上的點,且OC∥BD,AD分別與BC,OC相交于點E,F,則下列結論:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
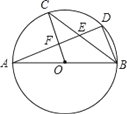
A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO繞點O旋轉150°后得到△A1B1O,則點A1的坐標為
,AB=1,把△ABO繞點O旋轉150°后得到△A1B1O,則點A1的坐標為

A.(﹣1,![]() ) B.(﹣1,
) B.(﹣1,![]() )或(﹣2,0) C.(
)或(﹣2,0) C.(![]() ,﹣1)或(0,﹣2) D.(
,﹣1)或(0,﹣2) D.(![]() ,﹣1)
,﹣1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com