
 ?若存在,求對應的x值;若不存在,說明理由.
?若存在,求對應的x值;若不存在,說明理由. •
• x•
x• x=
x= x2(0<x<4);
x2(0<x<4); ×8×4=16,當A′在BC上時,x=4,y=4,
×8×4=16,當A′在BC上時,x=4,y=4, 不在這個范圍內,所以這時不存在直線MN.
不在這個范圍內,所以這時不存在直線MN.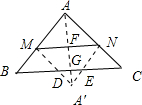 當A′在△ABC外部時,連AA′交MN于F,交BC于G,且A′F=AF=
當A′在△ABC外部時,連AA′交MN于F,交BC于G,且A′F=AF= x,
x, x,
x, x-4+
x-4+ x=x-4,
x=x-4, (x+2x-8)×(4-
(x+2x-8)×(4- x)=-
x)=- x2+8x-16(其中4<x<8),
x2+8x-16(其中4<x<8), 時,
時, x2+8x-16=
x2+8x-16= ,
, ,
, ,
, .
.

科目:初中數學 來源: 題型:
 把兩個全等的等腰直角三角形ABC和EFG(其直角邊長均為4)疊放在一起(如圖①),且使三角板EFG的直角頂點G與三角板ABC的斜邊中點O重合.現將三角板EFG繞O點逆時針旋轉(旋轉角α滿足條件:0°<α<90°),四邊形CHGK是旋轉過程中兩三角板的重疊部分(如圖②).
把兩個全等的等腰直角三角形ABC和EFG(其直角邊長均為4)疊放在一起(如圖①),且使三角板EFG的直角頂點G與三角板ABC的斜邊中點O重合.現將三角板EFG繞O點逆時針旋轉(旋轉角α滿足條件:0°<α<90°),四邊形CHGK是旋轉過程中兩三角板的重疊部分(如圖②).| 5 | 16 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
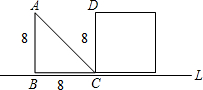 AB與CD重合.設x秒時,三角形與正方形不重疊部分的面積為ym2.
AB與CD重合.設x秒時,三角形與正方形不重疊部分的面積為ym2.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,等腰直角三角形△ABC中,∠ACB=90°,點D是BC的中點,CE⊥AD于點F交AB于點E,CH是AB上的高交AD于點G.
如圖,等腰直角三角形△ABC中,∠ACB=90°,點D是BC的中點,CE⊥AD于點F交AB于點E,CH是AB上的高交AD于點G.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com