
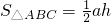 ,即三角形面積等于水平寬與鉛垂高乘積的一半.
,即三角形面積等于水平寬與鉛垂高乘積的一半.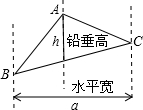
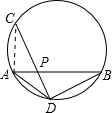
 S△CAB,若存在,求出P點的坐標;若不存在,請說明理由.
S△CAB,若存在,求出P點的坐標;若不存在,請說明理由.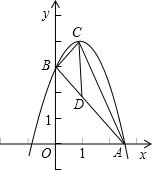
 =
=
 =
=

 S△CAB
S△CAB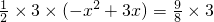 ,化簡得:4x2-12x+9=0
,化簡得:4x2-12x+9=0 ,
, 代入y1=-x2+2x+3中,
代入y1=-x2+2x+3中,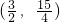
 S△CAB即可得到一個關于點P的橫坐標的方程,即可求出x的值.進而得到P點的坐標.
S△CAB即可得到一個關于點P的橫坐標的方程,即可求出x的值.進而得到P點的坐標.

科目:初中數(shù)學 來源: 題型:
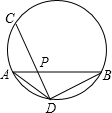
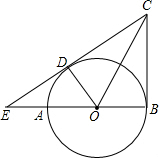 如圖,AB是⊙O的直徑,CB、CE分別切⊙O于點B、D,CE與BA的延長線交于點E,連接OC、OD.
如圖,AB是⊙O的直徑,CB、CE分別切⊙O于點B、D,CE與BA的延長線交于點E,連接OC、OD.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
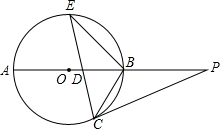 PA上截取PD=PC,連接CD,并延長交⊙O于點E.
PA上截取PD=PC,連接CD,并延長交⊙O于點E.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
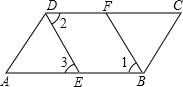
 19、如圖,AB⊥AC,CD、BE分別是△ABC的角平分線,AG∥BC,AG⊥BG,下列結論:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正確的結論是( )
19、如圖,AB⊥AC,CD、BE分別是△ABC的角平分線,AG∥BC,AG⊥BG,下列結論:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正確的結論是( )查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com