
【題目】已知關于x的一元二次方程x2﹣3x+m﹣2=0有兩個實數根x1,x2.
(1)求m的取值范圍;
(2)若x1,x2滿足2x1=|x2|+1,求m的值.
【答案】(1)m≤![]() (2)
(2)![]() 或﹣8
或﹣8
【解析】
(1)根據根的判別式即可求解;
(2)根據根與系數的關系,分情況討論即可求得m的值.
解:(1)∵關于x的一元二次方程x2﹣3x+m﹣2=0有兩個實數根,
∴△≥0,即9﹣4(m﹣2)≥0
解得m≤![]() .
.
答:m的求值范圍為m≤![]() .
.
(2))根據根與系數的關系:
x1+x2=3,x1x2=m﹣2,
∵x1,x2滿足2x1=|x2|+1,
①當x2≥0時,2x1=x2+1
把x2=3﹣x1代入,得
2x1=3﹣x1+1
解得x1=![]() ,
,
∴x2=![]() ,
,
∴m﹣2=x1x2=![]()
∴m=![]() .
.
②當x2≤0時,2x1=﹣x2+1
∴2x1+3﹣x1=1
解得x1=﹣2,x2=5,
∴m﹣2=﹣10
m=﹣8.
答:m的值為![]() 或﹣8
或﹣8


科目:初中數學 來源: 題型:
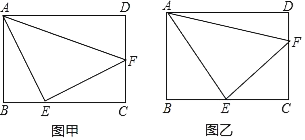
【題目】在矩形ABCD中,AB=3,BC=4,點E、F分別在BC與CD上,且∠EAF=45°.如圖甲,若EA=EF,則EF=_____;如圖乙,若CE=CF,則EF=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,對于點P(x,y),如果點Q(x,y′)的縱坐標滿足y′=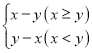 ,那么稱點Q為點P的“關聯點”.
,那么稱點Q為點P的“關聯點”.
(1)請直接寫出點(3,5)的“關聯點”的坐標 ;
(2)如果點P在函數y=x﹣2的圖象上,其“關聯點”Q與點P重合,求點P的坐標;
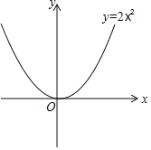
(3)如果點M(m,n)的“關聯點”N在函數y=2x2的圖象上,當0≤m≤2時,求線段MN的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列一組圖形,它反映了圖形中點的個數與第![]() 個圖形之間的某種變化規律.
個圖形之間的某種變化規律.
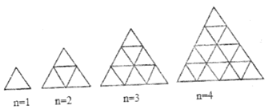
(1)填寫下表:
第 | 1 | 2 | 3 | 4 | … |
圖形中所有點的個數 | … |
(2)設第![]() 個圖形中點的個數是
個圖形中點的個數是![]() 個,試寫出
個,試寫出![]() 與
與![]() 的關系式 .
的關系式 .
(3)若某個圖形中所有點的個數是66個,求這是第幾個圖形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有這樣一個問題:探究函數y=![]() 的圖象與性質.小美根據學習函數的經驗,對函數y=
的圖象與性質.小美根據學習函數的經驗,對函數y=![]() 的圖象與性質進行了探究下面是小美的探究過程,請補充完整:
的圖象與性質進行了探究下面是小美的探究過程,請補充完整:
(1)函數y=![]() 的自變量x的取值范圍是 ;
的自變量x的取值范圍是 ;
(2)下表是y與x的幾組對應值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
|
| m |
|
| … |
求m的值;
(3)如圖,在平面直角坐標系xOy中,描出了以上表中各對對應值為坐標的點.根據描出的點,畫出該函數的圖象;
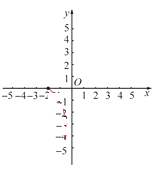
(4)結合函數的圖象,寫出該函數的一條性質: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,對稱軸為x=1,經過點(-1,0),有下列結論:①abc<0;②a+c>b;③3a+c=0;④a+b>m(am+b)(其中m≠1)其中正確的結論有( )
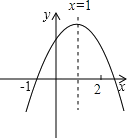
A. 1個
B. 2個
C. 3個
D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD是正方形,△ADF旋轉一定角度后得到△ABE,如圖所示,如果AF=3,AB=7,
求(1)指出旋轉中心和旋轉角度;
(2)求DE的長度;
(3)BE與DF的位置關系如何?請說明理由.
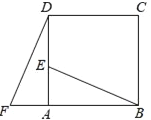
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,與y軸交于點C,對稱軸為直線x=1.直線y=﹣x+c與拋物線y=ax2+bx+c交于C、D兩點,則下列結論:
①abc>0
②a﹣b+c<0;
③2a+b+c>0;
④x(ax+b)≤a+b;
其中正確的有_____
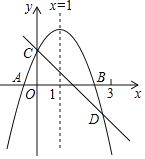
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據農業部提出“大力發展農村產業,實現鄉村全面振興”的方針,我市精確扶貧,指導某縣大力發展大五星枇杷種植,去年、今年枇杷產量連續獲得大豐收,該縣枇杷銷售采用線下銷售和線上銷售兩種模式.
(1)今年該縣種植專業戶大五星枇杷產量為4500千克,全部售出,其中線上銷售量不超過線下銷售的4倍,求該種植專業戶線下銷售量至少多少千克?
(2)該種植專業戶去年大五星枇杷線下銷售均價為10元/千克,銷售量為900千克,線上銷售均價為8元/千克,銷售量為1800千克,今年線下銷售均價上漲![]() ,但銷售量下降了
,但銷售量下降了![]() ,線上銷售均價上漲了
,線上銷售均價上漲了![]() ,銷量與去年持平,今年大五星枇杷的銷售總額比去年銷售總額減少了
,銷量與去年持平,今年大五星枇杷的銷售總額比去年銷售總額減少了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com