已知:在銳角△ABC中,AB=AC.D為底邊BC上一點,E為線段AD上一點,且∠BED=∠BAC=2∠DEC,連接CE.
(1)求證:∠ABE=∠DAC;
(2)若∠BAC=60°,試判斷BD與CD有怎樣的數量關系,并證明你的結論;
(3)若∠BAC=α,那么(2)中的結論是否還成立.若成立,請加以證明;若不成立,請說明理由.
【答案】
分析:(1)根據外角的性質,推出∠BED=∠ABE+∠BAE,由∠BAC=∠BAE+∠DAC,根據∠BED=∠BAC進行等量代換即可;
(2)在AD上截取AF=BE,連接CF,作CG∥BE交直線AD于G,∠BED=∠BAC,結合(1)所推出的結論,求證△ACF≌△BAE,根據全等三角形的性質、三角形內角和定理推出∠CFG=180°-∠AFC=180°-∠BEA=∠BED,由CG∥BE,可得∠CGF=∠BED,BD:CD=BE:CG,繼而推出∠CFG=∠CGF,即CG=CF,通過等量代換可得BE=AF=2CF,把比例式中的BE、CG用2CF、CF代換、整理后即可推出BD=2DC,總上所述BD與CD的數量關系與∠BAC的度數無關;
(3)根據(2)所推出的結論即可推出若∠BAC=α,那么(2)中的結論仍然還成立.
解答: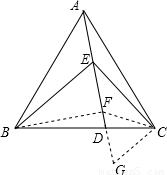
(1)證明:∵∠BED=∠ABE+∠BAE,∠BED=∠BAC,
∴∠ABE+∠BAE=∠BAC,
∵∠BAC=∠BAE+∠DAC,
∴∠DAC=∠ABE;
(2)解:在AD上截取AF=BE,連接CF,作CG∥BE交直線AD于G,∠BED=∠BAC,
∵∠FAC=∠ABE,
∴在△ACF和△BAE中,
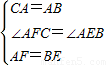
,
∴△ACF≌△BAE(SAS),
∴CF=AE,∠ACF=∠BAE,∠AFC=∠AEB.
∵∠ACF=∠BAE,∠AFC=∠BEA,
∴∠CFG=180°-∠AFC=180°-∠BEA=∠BED,
∵CG∥BE,
∴∠CGF=∠BED,
∴∠CFG=∠CGF,
∴CG=CF,
∵∠BED=2∠DEC,
∵∠CFG=∠DEC+∠ECF,∠CFG=∠BED,
∴∠ECF=∠DEC,
∴CF=EF,
∴BE=AF=2CF,
∵CG∥BE,
∴BD:CD=BE:CG,
∴BD:CD=2CF:CF=2,
∴BD=2DC,
∴BD與CD的數量關系與∠BAC的度數無關;
(3)解:∵BD與CD的數量關系與∠BAC的度數無關,
∴若∠BAC=α,那么(2)中的結論仍然還成立.
點評:本題主要考查等腰三角形的性質、全等三角形的判定與性質、平行線的性質、三角形內角和定理等知識點,關鍵在于正確地作出輔助線,求證相關的三角形全等,認真地進行等量代換.

 (1)證明:∵∠BED=∠ABE+∠BAE,∠BED=∠BAC,
(1)證明:∵∠BED=∠ABE+∠BAE,∠BED=∠BAC,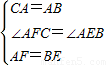 ,
,

 名校課堂系列答案
名校課堂系列答案 (即cosC=
(即cosC= ),則AC邊上的中線長是
.
),則AC邊上的中線長是
.