Question

已知：△ABC是邊長為4的等邊三角形，點O在邊AB上，⊙O過點B且分別與邊AB，BC相交于點D，E，EF⊥AC，垂足為F．

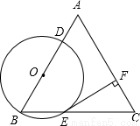
（1）求證：直線EF是⊙O的切線；

（2）當直線DF與⊙O相切時，求：⊙O的半徑．

Answer 1

（1）證明見解析；（2）.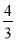

【解析】

試題分析：（1）連接OE．欲證直線EF是⊙O的切線，只需證明EF⊥AC．利用等邊三角形的三個內角都是60°、等腰三角形OBE以及三角形的內角和定理求得同位角∠BOE=∠A=60°，從而判定OE∥AC，所以由已知條件EF⊥AC判定OE⊥EF，即直線EF是⊙O的切線；

（2）連接DF．設⊙O的半徑是r．由等邊三角形的三個內角都是60°、三條邊都相等、以及在直角三角形中30°所對的直角邊是斜邊的一半求得關于r的方程4-r=2（4r-4），解方程即可．

試題解析：（1）證明：連接OE．

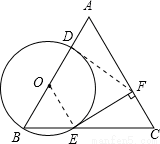
∵△ABC是等邊三角形，

∴∠A=∠B=∠C=60°；

在△BOE中，OB=OE，∠B=60°，

∴∠B=∠OEB=∠BOE=60°，

∴∠BOE=∠A=60°，

∴OE∥AC；

∵EF⊥AC，

∴OE⊥EF，即直線EF是⊙O的切線；

（2）【解析】
連接DF．

∵DF與⊙O相切，

∴∠ADF=90°．

設⊙O的半徑是r，則EB=r，EC=4-r，AD=4-2r．

在Rt△ADF中，∠A=60°，

∴AF=2AD=8-4r．

∴FC=4r-4；

在Rt△CEF中，∵∠C=60°，∴EC=2FC，

∴4-r=2（4r-4），

解得，r=；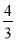

∴⊙O的半徑是．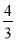

考點：1.切線的判定與性質；2.等邊三角形的判定與性質．