
【題目】已知:在平面直角坐標系中,點O為坐標原點,直線y=﹣x+3交x軸于點B,交y軸于點A,過點A作AC⊥AB交x軸于點C.
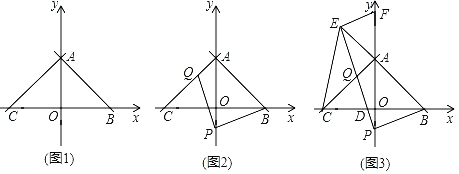
(1)如圖1,求直線AC的解析式;
(2)如圖2,點P在AO的延長線上,點Q在AC上,連接PB,PQ,且PQ=PB,設點P的縱坐標為t,AQ的長為d,求d與t之間的函數關系式(不要求寫出自變量t的取值范圍);
(3)如圖3,在(2)的條件下,PQ交x軸于點D,延長PQ交BA的延長線于點E,過點E作EF⊥PE交y軸于點F,若DE=![]() EF,求點Q的坐標.
EF,求點Q的坐標.
【答案】(1)AC的解析式為y=x+3;(2)d=﹣![]() t;(3)(﹣1,2)
t;(3)(﹣1,2)
【解析】
(1)先根據直線![]() 求出點A、B的坐標,從而可得OA、OB的長,再根據等腰直角三角形的判定與性質得出OC的長,從而可得點C的坐標,然后利用待定系數法求解即可;
求出點A、B的坐標,從而可得OA、OB的長,再根據等腰直角三角形的判定與性質得出OC的長,從而可得點C的坐標,然后利用待定系數法求解即可;
(2)先求出點P的坐標,再根據AQ的長、直線AC的解析式可求出點Q的坐標,然后根據![]() ,利用兩點之間的距離公式建立等式求解即可;
,利用兩點之間的距離公式建立等式求解即可;
(3)如圖(見解析),先求出點Q的坐標,從而得出PN、QN的長,再根據正切三角形函數值、勾股定理得出DP的長和![]() ,然后利用待定系數法求出直線PQ的解析式,聯立直線AB的解析式求出點E的坐標,最后利用兩點之間的距離公式求出DE的長,代入求解即可.
,然后利用待定系數法求出直線PQ的解析式,聯立直線AB的解析式求出點E的坐標,最后利用兩點之間的距離公式求出DE的長,代入求解即可.
(1)∵![]() 交x軸于點B,交y軸于點A
交x軸于點B,交y軸于點A
令![]() ,則
,則![]() ,解得
,解得![]()
∴![]()
令![]() ,則
,則![]()
∴![]()
∵![]() ,
,
∴![]()
∵![]()
![]()
∴![]()
![]()
∴![]()
設AC的解析式為![]()
將點![]() ,
,![]() 代入得
代入得![]() ,解得
,解得![]()
則直線AC的解析式為![]() ;
;
(2)∵點P在AO的延長線上,點P的縱坐標為t
∴![]() ,
,![]()
如圖,過點Q作![]() 軸交于點M
軸交于點M
∵AQ的長為![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]()
整理得![]()
解得![]() 或
或![]() (舍去)
(舍去)
故d與t之間的函數關系式為![]() ;
;
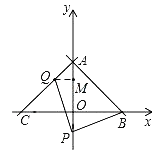
(3)如圖,過點Q作![]() 軸交于點N,則
軸交于點N,則![]()
∵![]()
![]()
∴![]() ,
,![]()
∴![]()
∴![]() ,即
,即![]()
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()
![]()
![]()
∴![]()
∴![]()
設直線PQ的解析式為![]()
將點![]() 代入得
代入得![]() ,解得
,解得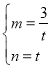
則直線PQ的解析式為![]()
聯立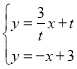 ,解得
,解得![]()
∴![]()
![]()
由兩點之間的距離公式得:![]()
將DE、DP的值代入![]() 得:
得: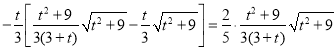
整理得:![]()
解得![]() 或
或![]() (不符題意,舍去)
(不符題意,舍去)
![]() .
.



科目:初中數學 來源: 題型:
【題目】已知:如圖,⊙O1和⊙O2相交于A、B兩點, ⊙O1經過點O2,點C在![]() 上運動(點C 不與A、B重合),AC的延長線交⊙O2于P,連結AB、BC、BP;
上運動(點C 不與A、B重合),AC的延長線交⊙O2于P,連結AB、BC、BP;
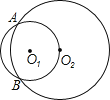
(1)按題意將圖形補充完整;
(2)當點C在![]() 上運動時,圖中不變的角有 (將符合要求的角都寫上)
上運動時,圖中不變的角有 (將符合要求的角都寫上)
(3)線段BC、PC的長度存在何種關系?寫出結論,并加以證明;
(4)設⊙O1和⊙O2的半徑為![]() 、
、![]() ,當
,當![]() ,
,![]() 滿足什么條件時,
滿足什么條件時,![]() 為等腰直角三角形?
為等腰直角三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 中,對角線
中,對角線![]() ,
,![]() 相交于點
相交于點![]() ,且
,且![]() ,
,![]() .動點
.動點![]() ,
,![]() 分別從點
分別從點![]() ,
,![]() 同時出發,運動速度均為lcm/s.點
同時出發,運動速度均為lcm/s.點![]() 沿
沿![]() 運動,到點
運動,到點![]() 停止.點
停止.點![]() 沿
沿![]() 運動,點
運動,點![]() 到點
到點![]() 停留4
停留4![]() 后繼續運動,到點
后繼續運動,到點![]() 停止.連接
停止.連接![]() ,
,![]() ,
,![]() ,設
,設![]() 的面積為
的面積為![]() (這里規定:線段是面積為0的三角形),點
(這里規定:線段是面積為0的三角形),點![]() 的運動時間為
的運動時間為![]() .
.
(1)求線段![]() 的長(用含
的長(用含![]() 的代數式表示);
的代數式表示);
(2)求![]() 時,求
時,求![]() 與
與![]() 之間的函數解析式,并寫出
之間的函數解析式,并寫出![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,直接寫出
時,直接寫出![]() 的取值范圍.
的取值范圍.
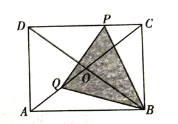
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四張卡片,除一面分別寫有數字2,2,3,6外,其余均相同,將卡片洗勻后,寫有數字的一面朝下扣在桌面上,隨機抽取一張卡片記下數字后放回,洗勻后仍將寫有數字的一面朝下扣在桌面上,再抽取一張.
(1)用列表或畫樹狀圖的方法求兩次都恰好抽到2的概率;
(2)小貝和小晶以此為游戲,游戲規則是:第一次抽取的數字作為十位,第二次抽取的數字作為個位,組成一個兩位數,若組成的兩位數不小于32,小貝獲勝,否則小晶獲勝.你認為這個游戲公平嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1,圖2分別是10×6的網格,網格中每個小正方形的邊長均為1,每個網格中畫有一個平行四邊形,請分別在圖1,圖2中各畫一條線段,各圖均滿足以下要求:
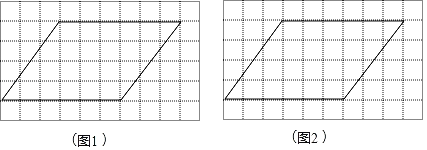
(1)線段的一個端點為平行四邊形的頂點,另一個端點在平行四邊形一邊的格點上(每個小正方形的頂點均為格點);
(2)將平行四邊形分割成兩個圖形,都要求其中一個是軸對稱圖形,圖1,圖2的分法不相同.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王輝在某景區經營一個小攤位,他以10元/根的價格購進一批登山杖,經市場調查發現當售價為24元/根時,每天可出售156根,此后售價每增加5元,就會少售出30根.
(1)求登山杖的單根售價![]() (元)與銷售數量
(元)與銷售數量![]() (根)之間的函數關系式;
(根)之間的函數關系式;
(2)若設王輝每天的日銷售利潤為![]() 元,求
元,求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(3)為了避免惡性競爭且保障商家獲得一定利潤,景區管理處規定登山杖的銷售單價不得低于32元且不高于36元,則王輝的日銷售利潤最大是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 經過點兩點
經過點兩點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是拋物線上一個動點,設點
是拋物線上一個動點,設點![]() 的橫坐標為
的橫坐標為![]() .連接
.連接![]()
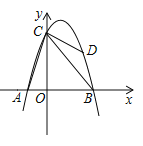
(1)求拋物線的函數表達式;
(2)當![]() 的面積等于
的面積等于![]() 的面積時,求
的面積時,求![]() 的值;
的值;
(3)當![]() 時,若點
時,若點![]() 是
是![]() 軸正半軸上上的一個動點,點
軸正半軸上上的一個動點,點![]() 是拋物線上動點,試判斷是否存在這樣的點
是拋物線上動點,試判斷是否存在這樣的點![]() ,使得以點
,使得以點![]() 為頂點的四邊形是平行四邊形.若存在,請直接寫出點
為頂點的四邊形是平行四邊形.若存在,請直接寫出點![]() 的坐標:若不存在,請說明理由.
的坐標:若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com