
【題目】王輝在某景區經營一個小攤位,他以10元/根的價格購進一批登山杖,經市場調查發現當售價為24元/根時,每天可出售156根,此后售價每增加5元,就會少售出30根.
(1)求登山杖的單根售價![]() (元)與銷售數量
(元)與銷售數量![]() (根)之間的函數關系式;
(根)之間的函數關系式;
(2)若設王輝每天的日銷售利潤為![]() 元,求
元,求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(3)為了避免惡性競爭且保障商家獲得一定利潤,景區管理處規定登山杖的銷售單價不得低于32元且不高于36元,則王輝的日銷售利潤最大是多少元?
【答案】(1)y=-6x+300;(2)W=-6![]() +2400;(3)當售價定為32元時,王輝的日銷售利潤最大,且最大利潤為2376元.
+2400;(3)當售價定為32元時,王輝的日銷售利潤最大,且最大利潤為2376元.
【解析】
(1)根據銷售單價和銷售量之間的關系,列出函數關系式y=156-![]() 化簡即可;
化簡即可;
(2)根據日銷售利潤=單根利潤×數量,可得出函數關系式W=-6![]() +2400,化簡整理即可;
+2400,化簡整理即可;
(3)由(2)中結論,利用二次函數的最值問題,結合單價的取值范圍,即可求出結果.
(1)依據題意得,y與x的函數關系式為:y=156-![]() ,
,
整理,得y=-6x+300,
答:所求y與x的函數關系式為:y=-6x+300,
故答案為:y=-6x+300;
(2)依據日銷售利潤=單根利潤×數量,得W與x的函數關系式為:W=(x-10)(-6x+300),
整理得W=-6![]() +2400,
+2400,
答:日銷售利潤W和x的函數關系式為:W=-6![]() +2400,
+2400,
故答案為:W=-6![]() +2400;
+2400;
(3)∵W=-6![]() +2400,a=-6<0,
+2400,a=-6<0,
∴x>30,W隨x的增加而減小,
∵銷售單價不得低于32元且不高于36元,
∴當x=32時,W有最大值,且最大值為W=-6![]() +2400=2376(元),
+2400=2376(元),
答:當售價定為32元時,王輝的日銷售利潤最大,且最大利潤為2376元,
故答案為:2376.


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°.
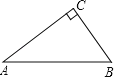
(1)以AB邊上一點O為圓心作⊙O,使⊙O經過點A,C;(保留作圖痕跡,不寫作法)
(2)判斷點B與⊙O的位置關系是 .(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小敏參加答題游戲,答對最后兩道單選題就順利通關.第一道單選題有3個選項![]() ,
,![]() ,
,![]() ,第二道單選題有4個選項
,第二道單選題有4個選項![]() ,
,![]() ,
,![]() ,
,![]() ,這兩道題小敏都不會,不過小敏還有一個“求助”機會,使用“求助”可以去掉其中一道題的一個錯誤選項.假設第一道題的正確選項是
,這兩道題小敏都不會,不過小敏還有一個“求助”機會,使用“求助”可以去掉其中一道題的一個錯誤選項.假設第一道題的正確選項是![]() ,第二道題的正確選項是
,第二道題的正確選項是![]() ,解答下列問題:
,解答下列問題:
(1)如果小敏第一道題不使用“求助”,那么她答對第一道題的概率是________;
(2)如果小敏將“求助”留在第二道題使用,用畫樹狀圖或列表的方法,求小敏順利通關的概率;
(3)小敏選第________道題(選“一”或“二”)使用“求助”,順利通關的可能性更大.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小魯在一個不透明的盒子里裝了5個除顏色外其他都相同的小球,其中有3個是紅球,2個是綠球,每次拿一個球然后放回去,拿2次,則至少有一次取到綠球的概率是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,點O為坐標原點,直線y=﹣x+3交x軸于點B,交y軸于點A,過點A作AC⊥AB交x軸于點C.
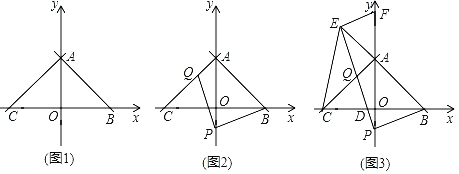
(1)如圖1,求直線AC的解析式;
(2)如圖2,點P在AO的延長線上,點Q在AC上,連接PB,PQ,且PQ=PB,設點P的縱坐標為t,AQ的長為d,求d與t之間的函數關系式(不要求寫出自變量t的取值范圍);
(3)如圖3,在(2)的條件下,PQ交x軸于點D,延長PQ交BA的延長線于點E,過點E作EF⊥PE交y軸于點F,若DE=![]() EF,求點Q的坐標.
EF,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線AC與BD交于點O,點E在AD上,且DE=CD,連接OE,∠ABE=![]() ∠ACB,若AE=2,則OE的長為_____.
∠ACB,若AE=2,則OE的長為_____.
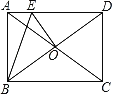
查看答案和解析>>
科目:初中數學 來源: 題型:
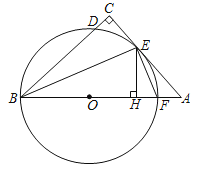
【題目】如圖,在△ABC中,∠C=90°,∠ABC的平分線交AC于點E,過點E作BE的垂線交AB于點F,⊙O是△BEF的外接圓.
(1)求證:AC是⊙O的切線;
(2)過點E作EH⊥AB,垂足為H,若CD=1,EH=3,求BE長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,點E、F分別在邊AB和CD上,下列條件不能判定四邊形DEBF一定是平行四邊形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com