
【題目】等腰![]() 被某一條直線分成兩個等腰三角形,并且其中一個等腰三角形與原三角形相似,則等腰
被某一條直線分成兩個等腰三角形,并且其中一個等腰三角形與原三角形相似,則等腰![]() 的頂角的度數是____.
的頂角的度數是____.
【答案】![]() 或
或![]() 或
或![]()
【解析】
因為題中沒有指明是過頂角的頂點還是過底角的頂點,且其中一個等腰三角形與原三角形相似與故應該分三種情況進行分析,從而求解.
解:①如圖1,∵AB=AC,當BD=CD,CD=AD,
∴∠B=∠C=∠BAD=∠CAD,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠B=45°,
∴∠BAC=90°.
此時易知∠BDA=∠BAC=90°,∠ABD=∠ABC= 45°,故![]() ∽
∽![]() ;
;
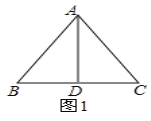
②如圖2,∵AB=AC,AD=BD,AC=CD,
∴∠B=∠C=∠BAD,∠CAD=∠CDA,
∵∠CDA=∠B+∠BAD=2∠B,
∴∠BAC=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BAC=108°.
此時易知∠BDA=∠BAC=108°,∠ABD=∠ABC= 36°, 故![]() ∽
∽![]() ;
;
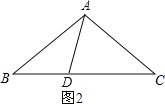
③如圖3,∵AB=AC,AD=BD=BC,
∴∠B=∠C,∠BAC=∠ABD,∠BDC=∠C,
∵∠BDC=∠A+∠ABD=2∠BAC,
∴∠ABC=∠C=2∠BAC,
∵∠BAC+∠ABC+∠C=180°,
∴5∠BAC=180°,
∴∠BAC=36°.
此時易知∠CBA=∠CDB=72°,∠BAC=∠DBC=36°,故有![]() ∽
∽![]() ;
;
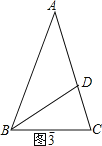
故答案為:![]() 或
或![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】某數學活動小組在一次活動中,對一個數學問題作如下探究:
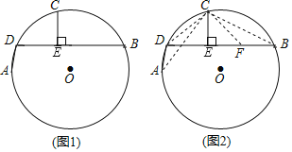
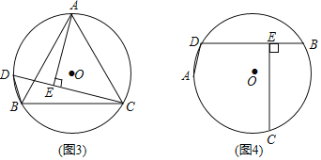
(問題發現)如圖1,AD,BD為⊙O的兩條弦(AD<BD),點C為![]() 的中點,過C作CE⊥BD,垂足為E.求證:BE=DE+AD.
的中點,過C作CE⊥BD,垂足為E.求證:BE=DE+AD.
(問題探究)小明同學的思路是:如圖2,在BE上截取BF=AD,連接CA,CB,CD,CF.……請你按照小明的思路完成上述問題的證明過程.
(結論運用)如圖3,△ABC是⊙O的內接等邊三角形,點D是![]() 上一點,∠ACD=45°,連接BD,CD,過點A作AE⊥CD,垂足為E.若AB=
上一點,∠ACD=45°,連接BD,CD,過點A作AE⊥CD,垂足為E.若AB=![]() ,則△BCD的周長為 .
,則△BCD的周長為 .
(變式探究)如圖4,若將(問題發現)中“點C為![]() 的中點”改為“點C為優弧
的中點”改為“點C為優弧![]() 的中點”,其他條件不變,上述結論“BE=DE+AD”還成立嗎?若成立,請說明理由;若不成立,請寫出BE、AD、DE之間的新等量關系,并加以證明.
的中點”,其他條件不變,上述結論“BE=DE+AD”還成立嗎?若成立,請說明理由;若不成立,請寫出BE、AD、DE之間的新等量關系,并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() ),連接
),連接![]() 、
、![]() ,點
,點![]() 為線段
為線段![]() 的中點,連接
的中點,連接![]() 、
、![]() ,
,![]() 繞點
繞點![]() 順時針旋轉,探究線段
順時針旋轉,探究線段![]() 與
與![]() 的數量關系.
的數量關系.
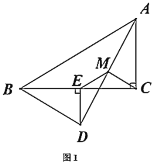
(1)如圖1,點![]() 落在
落在![]() 邊上時,探究
邊上時,探究![]() 與
與![]() 的數量關系,并說明理由;
的數量關系,并說明理由;
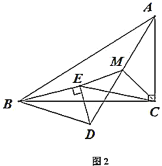
(2)如圖2,點![]() 落在
落在![]() 內部時,探究
內部時,探究![]() 與
與![]() 的數量關系,并說明理由;
的數量關系,并說明理由;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在春節來臨之際,小楊的服裝小店用2500元購進了一批時尚圍巾,上市后很快售完,小楊又用8400元購進第二批這種圍巾,所購數量是第一批購進數量的3倍,但每條圍巾的進價多了3元.
(1)小楊兩次共購進這種圍巾多少條?
(2)如果這兩批圍巾每條的售價相同,且全部售完后總利潤率不低于20%,那么每條圍巾的售價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王輝在某景區經營一個小攤位,他以10元/根的價格購進一批登山杖,經市場調查發現當售價為24元/根時,每天可出售156根,此后售價每增加5元,就會少售出30根.
(1)求登山杖的單根售價![]() (元)與銷售數量
(元)與銷售數量![]() (根)之間的函數關系式;
(根)之間的函數關系式;
(2)若設王輝每天的日銷售利潤為![]() 元,求
元,求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(3)為了避免惡性競爭且保障商家獲得一定利潤,景區管理處規定登山杖的銷售單價不得低于32元且不高于36元,則王輝的日銷售利潤最大是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市擬于中秋節前![]() 天里銷售某品牌月餅,其進價為
天里銷售某品牌月餅,其進價為![]() 元/
元/![]() .設第
.設第![]() 天的銷售價格為
天的銷售價格為![]() (元/
(元/![]() )銷售量為
)銷售量為![]() .該超市根據以往的銷售經驗得出以下的銷售規律:①與
.該超市根據以往的銷售經驗得出以下的銷售規律:①與![]() 滿足一次函數關系,且當
滿足一次函數關系,且當![]() 時,
時,![]() ;
;![]() 時,
時,![]() .②
.②![]() 與
與![]() 的關系為
的關系為![]() .
.
(1)![]() 與
與![]() 的關系式為________;
的關系式為________;
(2)當![]() 時,求第幾天的銷售利潤
時,求第幾天的銷售利潤![]() (元)最大?最大利潤為多少?
(元)最大?最大利潤為多少?
(3)若在當天銷售價格的基礎上漲![]() 元/
元/![]() ,在第
,在第![]() 天至
天至![]() 天銷售利潤最大值為
天銷售利潤最大值為![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC 內接于⊙O,過點 A 作⊙O 的切線交 CB 的延長線于點 P,且∠PAB=45°.
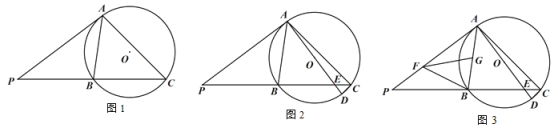
(1)如圖 1,求∠ACB 的度數;
(2)如圖 2,AD 是⊙O 的直徑,AD 交 BC 于點 E,連接 CD,求證:AC CD ![]() ;
;
(3)如圖 3 ,在(2)的條件下,當 BC 4![]() CD 時,點 F,G 分別在 AP,AB 上,連接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的長.
CD 時,點 F,G 分別在 AP,AB 上,連接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】抗擊疫情,眾志成城,舉國上下,共克時艱.為確定應對疫情影響穩外貿穩外資的新舉措,國務院總理李克強 3 月 10 日主持召開國務院常務會議,要求更好發揮專項再貸款再貼 現政策作用,支持疫情防控保供和企業紓困發展.會議指出,近段時間,有關部門按照國務 院要求,引導金融機構實施![]() 億元專項再貸款政策,以優惠利率資金有力支持了疫情防 控物資保供、農業和企業特別是小微企業復工復產.要進一步把政策落到位,加快貸款投放 進度,更好保障防疫物資保供、春耕備耕、國際供應鏈產品生產、勞動密集型產業、中小微 企業等資金需求.數據
億元專項再貸款政策,以優惠利率資金有力支持了疫情防 控物資保供、農業和企業特別是小微企業復工復產.要進一步把政策落到位,加快貸款投放 進度,更好保障防疫物資保供、春耕備耕、國際供應鏈產品生產、勞動密集型產業、中小微 企業等資金需求.數據![]() 億元用科學記數法表示為( )
億元用科學記數法表示為( )
A.![]() 元B.
元B.![]() 元C.
元C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司投入研發費用40萬元(40萬元只計入第一年成本),成功研發出一種產品.公司按訂單生產(產量=銷售量),第一年該產品正式投產后,生產成本為4元/件.此產品年銷售量y(萬件)與售價x(元件)之間滿足函數關系式y=﹣x+20.
(1)求這種產品第一年的利潤W(萬元)與售價x(元件)滿足的函數關系式;
(2)該產品第一年的利潤為24萬元,那么該產品第一年的售價是多少?
(3)第二年,該公司將第一年的利潤24萬元(24萬元只計入第二年成本)再次投入研發,使產品的生產成本降為3元/件.為保持市場占有率,公司規定第二年產品售價不超過第一年的售價,另外受產能限制,銷售量無法超過10萬件.請計算該公司第二年的利潤W2至少為多少萬元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com