【題目】如圖，已知B、C、E三點在同一條直線上，△ABC與△DCE都是等邊三角形.其中線段BD交AC于點G，線段AE交CD于點F.
求證：（1）△ACE≌△BCD；（2）△GFC是等邊三角形.
【答案】（1）證明見解析；（2）證明見解析.
【解析】試題分析：1）利用等邊三角形的性質得出條件，可證明：△ACE≌△BCD；
（2）利用△ACE≌△BCD得出∠CBG=∠CAF，再運用平角定義得出∠BCG=∠ACF進而得出△BCG≌△ACF,因此CG=CF，再由∠ACF=60°根據“有一個角是60°的三角形是等邊三角形可得△GFC是等邊三角形．
試題解析：證明：（1）∵△ABC和△CDE都是等邊三角形，
∴∠BCA=∠DCE=60°，BC=AC=AB，EC=CD=ED，
∴∠BCD=∠ACE，
在△BCD和△ACE中，
,
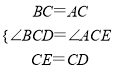∴△ACE≌△BCD；
（2）∵△BCD≌△ACE，
∴∠CBG=∠CAF．
∵∠ACB=∠DCE=60°，
∴∠ACF=60°．
∴∠BCG=∠ACF，
在△BCG和△ACF中，
，
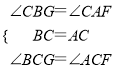∴△BCG≌△ACF（ASA），
∴CG=CF；
∵∠ACF=60°，
∴△GFC是等邊三角形．
世紀百通期末金卷系列答案科目：初中數學 來源： 題型：
【題目】下列說法中，正確的是（ ）
A.正數和負數統稱為有理數
B.0是最小的有理數
C.如果兩個數的絕對值相等，那么這兩個數一定相等
D.互為相反數的兩個數之和為零
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A.一個數的絕對值一定大于它的本身
B.只有正數的絕對值是它的本身
C.負數的絕對值是它的相反數
D.一個數的絕對值是它的相反數，則這個數一定是負數
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，∠C=Rt∠，AB=5cm，BC=3cm，若動點P從點C開始，按C→A→B→C的路徑運動，且速度為每秒1cm，設出發的時間為t秒．
（1）出發2秒后，求△ABP的周長．
（2）問t滿足什么條件時，△BCP為直角三角形？
（3）另有一點Q，從點C開始，按C→B→A→C的路徑運動，且速度為每秒2cm，若P、Q兩點同時出發，當P、Q中有一點到達終點時，另一點也停止運動．當t為何值時，直線PQ把△ABC的周長分成相等的兩部分？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點
的坐標
，點
的坐標
，點
的坐標
，點
的坐標
，如圖①，另有一點
從點
出發，沿著
運動，到點
停止．
（
）當
在
上時， 
__________．
（
）點
在運動過程中，直接寫出可以和
形成等腰三角形的點的坐標．
（
）將圖①中的長方形在坐標平面內繞原點按逆時針方向旋轉
，如圖②，求出此時點
、
、
的坐標?
查看答案和解析>>
科目：初中數學 來源： 題型：
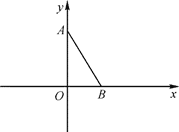
【題目】如圖，平面直角坐標系 xOy 中，已知點 A(0，3)，點 B(
，0)，連接 AB．若對于平 面內一點 C，當△ABC 是以 AB 為腰的等腰三角形時，稱點 C 是線段 AB 的“等長點”
(1)在點 C1 (－2， 
)，點 C2 (0，－2)，點 C3 (
， 
)中，線段 AB 的“等長點”是點______________；
(2)若點 D( m ， n )是線段 AB 的“等長點”，且∠DAB＝60，求 m 和 n 的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
