
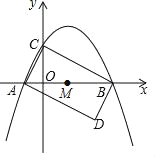
【題目】如圖,拋物線y=ax2+bx+2與x軸相交于A(﹣1,0),B(4,0)兩點,與y軸相交于點C.
(1)求拋物線的解析式;
(2)將△ABC繞AB中點M旋轉180°,得到△BAD.
①求點D的坐標;
②判斷四邊形ADBC的形狀,并說明理由;
(3)在該拋物線對稱軸上是否存在點P,使△BMP與△BAD相似?若存在,請求出所有滿足條件的P點的坐標;若不存在,請說明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①點D的坐標為(3,﹣2),②四邊形ADBC為矩形,理由見解析;(3)在該拋物線對稱軸上存在點P,使△BMP與△BAD相似,點P的坐標為(
x+2;(2)①點D的坐標為(3,﹣2),②四邊形ADBC為矩形,理由見解析;(3)在該拋物線對稱軸上存在點P,使△BMP與△BAD相似,點P的坐標為(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).
【解析】
(1)由點A、B的坐標,利用待定系數法即可求出拋物線的解析式;
(2)利用二次函數圖象上點的坐標特征可求出點C的坐標.①過點D作DE⊥x軸于點E,根據旋轉的性質可得出OA=EB、OC=ED,結合點A、B、O、C的坐標,即可找出點D的坐標;②由點A、B、C的坐標可得出OA、OC、OB的長度,利用勾股定理可求出AC、BC的長,由AC2+BC2=25=AB2可得出∠ACB=90°,再利用旋轉的性質即可找出四邊形ADBC為矩形;
(3)假設存在,設點P的坐標為(![]() ,m),由點M為AB的中點可得出∠BPD=∠ADB=90°,分△PMB∽△BDA及△BMP∽△BDA兩種情況考慮,利用相似三角形的性質可得出關于m的含絕對值的一元一次方程,解之即可得出結論.
,m),由點M為AB的中點可得出∠BPD=∠ADB=90°,分△PMB∽△BDA及△BMP∽△BDA兩種情況考慮,利用相似三角形的性質可得出關于m的含絕對值的一元一次方程,解之即可得出結論.
(1)將A(﹣1,0)、B(4,0)代入y=ax2+bx+2,得:![]() ,解得:
,解得:![]() ,
,
∴拋物線的解析式為y=﹣![]() x2+
x2+![]() x+2.
x+2.
(2)當x=0時,y=﹣![]() x2+
x2+![]() x+2=2,
x+2=2,
∴點C的坐標為(0,2).
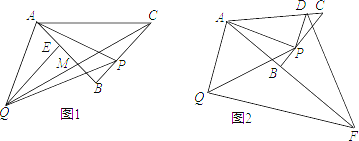
①過點D作DE⊥x軸于點E,如圖1所示.
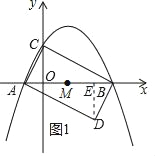
∵將△ABC繞AB中點M旋轉180°,得到△BAD,
∴OA=EB,OC=ED.
∵A(﹣1,0),O(0,0),C(0,2),B(4,0),
∴BE=1,DE=2,OE=3,
∴點D的坐標為(3,﹣2).
②四邊形ADBC為矩形,理由如下:
∵A(﹣1,0),B(4,0),C(0,2),
∴OA=1,OC=2,OB=4,AB=5,
∴AC=![]() ,BC=
,BC=![]() .
.
∵AC2+BC2=25=AB2,
∴∠ACB=90°.
∵將△ABC繞AB中點M旋轉180°,得到△BAD,
∴∠ABC=∠BAD,BC=AD,
∴BC∥AD且BC=AD,
∴四邊形ADBC為平行四邊形.
又∵∠ACB=90°,
∴四邊形ADBC為矩形.
(3)假設存在,設點P的坐標為(![]() ,m).
,m).
∵點M為AB的中點,
∴∠BPD=∠ADB=90°,
∴有兩種情況(如圖2所示).
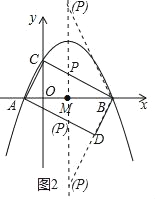
①當△PMB∽△BDA時,有![]() ,即
,即![]() ,
,
解得:m=±![]() ,
,
∴點P的坐標為(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() );
);
②當△BMP∽△BDA時,有![]() ,即
,即![]() ,
,
解得:m=±5,
∴點P的坐標為(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).
綜上所述:在該拋物線對稱軸上存在點P,使△BMP與△BAD相似,點P的坐標為(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案科目:初中數學 來源: 題型:
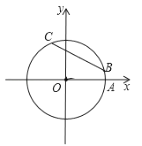
【題目】如圖,在平面直角坐標系xOy中,以原點O為圓心的圓過點A(![]() ,0),直線y=kx-2k+3與⊙O交于B、C兩點,則弦BC的長的最小值為_______.
,0),直線y=kx-2k+3與⊙O交于B、C兩點,則弦BC的長的最小值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
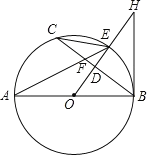
【題目】如圖,AB為⊙O的直徑,OD⊥弦BC于點D,交⊙O于點E,AE與BC交于點F,點H為OD延長線上一點,且∠OHB=∠AEC.
(1)求證:BH是⊙O的切線;
(2)求證:CE2=EF·EA;
(3)若⊙O的半徑為5,sin∠C=![]() ,求BF的長.
,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
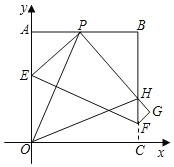
【題目】如圖,將一張邊長為8的正方形紙片OABC放在直角坐標系中,使得OA與y軸重合,OC與x軸重合,點P為正方形AB邊上的一點(不與點A、點B重合).將正方形紙片折疊,使點O落在P處,點C落在G處,PG交BC于H,折痕為EF.連接OP、OH.
初步探究
(1)當AP=4時
①直接寫出點E的坐標 ;
②求直線EF的函數表達式.
深入探究
(2)當點P在邊AB上移動時,∠APO與∠OPH的度數總是相等,請說明理由.
拓展應用
(3)當點P在邊AB上移動時,△PBH的周長是否發生變化?并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
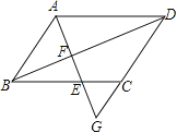
【題目】如圖,在平行四邊形ABCD中,點G在邊DC的延長線上,AG交邊BC于點E,交對角線BD于點F.
(1)求證:AF2=EFFG;
(2)如果EF=![]() ,FG=
,FG=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(閱讀材科)小明同學發現這樣一個規律:兩個頂角相等的等腰三角形,
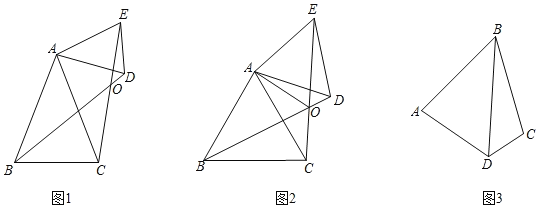
如果具有公共的項角的頂點,并把它們的底角頂點連接起來則形成一組全等的三角形,小明把具有這個規律的圖形稱為“手拉手”圖形.如圖1,在“手拉手”圖形中,小明發現若∠BAC=∠DAE,AB=AC,AD=AE,則△ABD≌△ACE.
(材料理解)(1)在圖1中證明小明的發現.
(深入探究)(2)如圖2,△ABC和△AED是等邊三角形,連接BD,EC交于點O,連接AO,下列結論:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正確的有 .(將所有正確的序號填在橫線上).
(延伸應用)(3)如圖3,AB=BC,∠ABC=∠BDC=60°,試探究∠A與∠C的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,![]() 為等腰三角形,
為等腰三角形,![]() ,點
,點![]() 在線段
在線段![]() 上(不與
上(不與![]() 重合),以
重合),以![]() 為腰長作等腰直角
為腰長作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求證:![]() ;
;
(2)連接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如圖2,過![]() 作
作![]() 于
于![]() 的延長線于點
的延長線于點![]() ,過
,過![]() 點作
點作![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,當點
,當點![]() 在線段
在線段![]() 上運動時(不與
上運動時(不與![]() 重合),式子
重合),式子![]() 的值會變化嗎?若不變,求出該值;若變化,請說明理由..
的值會變化嗎?若不變,求出該值;若變化,請說明理由..
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 朗讀者
朗讀者![]() 自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級
自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級![]() 、
、![]() 班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績
班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績![]() 滿分為100分
滿分為100分![]() 如圖所示.
如圖所示.
平均數 | 中位數 | 眾數 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根據圖示填寫表格;
根據圖示填寫表格;
![]() 結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
![]() 如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.
如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com