
【題目】如圖,已知△ABC內接于⊙O,點C在劣弧AB上(不與點A,B重合),點D為弦BC的中點,DE⊥BC,DE與AC的延長線交于點E,射線AO與射線EB交于點F,與⊙O交于點G,設∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,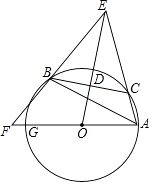
(1)點點同學通過畫圖和測量得到以下近似數據:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β關于ɑ的函數表達式,γ關于ɑ的函數表達式,并給出證明:
(2)若γ=135°,CD=3,△ABE的面積為△ABC的面積的4倍,求⊙O半徑的長.
【答案】
(1)
解:β=α+90°,γ=﹣α+180°
連接OB,

∴由圓周角定理可知:2∠BCA=360°﹣∠BOA,
∵OB=OA,
∴∠OBA=∠OAB=α,
∴∠BOA=180°﹣2α,
∴2β=360°﹣(180°﹣2α),
∴β=α+90°,
∵D是BC的中點,DE⊥BC,
∴OE是線段BC的垂直平分線,
∴BE=CE,∠BED=∠CED,∠EDC=90°
∵∠BCA=∠EDC+∠CED,
∴β=90°+∠CED,
∴∠CED=α,
∴∠CED=∠OBA=α,
∴O、A、E、B四點共圓,
∴∠EBO+∠EAG=180°,
∴∠EBA+∠OBA+∠EAG=180°,
∴γ+α=180°
(2)
解:當γ=135°時,此時圖形如圖所示,
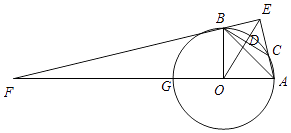
∴α=45°,β=135°,
∴∠BOA=90°,∠BCE=45°,
由(1)可知:O、A、E、B四點共圓,
∴∠BEC=90°,
∵△ABE的面積為△ABC的面積的4倍,
∴ ![]() ,
,
∴ ![]() ,
,
設CE=3x,AC=x,
由(1)可知:BC=2CD=6,
∵∠BCE=45°,
∴CE=BE=3x,
∴由勾股定理可知:(3x)2+(3x)2=62,
x= ![]() ,
,
∴BE=CE=3 ![]() ,AC=
,AC= ![]() ,
,
∴AE=AC+CE=4 ![]() ,
,
在Rt△ABE中,
由勾股定理可知:AB2=(3 ![]() )2+(4
)2+(4 ![]() )2,
)2,
∴AB=5 ![]() ,
,
∵∠BAO=45°,
∴∠AOB=90°,
在Rt△AOB中,設半徑為r,
由勾股定理可知:AB2=2r2,
∴r=5,
∴⊙O半徑的長為5.
【解析】(1)由圓周角定理即可得出β=α+90°,然后根據D是BC的中點,DE⊥BC,可知∠EDC=90°,由三角形外角的性質即可得出∠CED=α,從而可知O、A、E、B四點共圓,由圓內接四邊形的性質可知:∠EBO+∠EAG=180°,即γ=﹣α+180°;(2)由(1)及γ=135°可知∠BOA=90°,∠BCE=45°,∠BEC=90°,由于△ABE的面積為△ABC的面積的4倍,所以 ![]() ,根據勾股定理即可求出AE、AC的長度,從而可求出AB的長度,再由勾股定理即可求出⊙O的半徑r;
,根據勾股定理即可求出AE、AC的長度,從而可求出AB的長度,再由勾股定理即可求出⊙O的半徑r;
【考點精析】通過靈活運用余角和補角的特征和三角形的面積,掌握互余、互補是指兩個角的數量關系,與兩個角的位置無關;三角形的面積=1/2×底×高即可以解答此題.


科目:初中數學 來源: 題型:
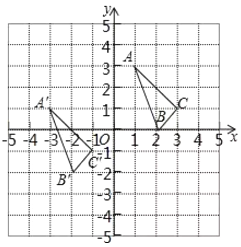
【題目】平面直角坐標系中,△ABC的三個頂點坐標分別為A(0,4),B(2,4),C(3,﹣1).
(1)試在平面直角坐標系中,標出A、B、C三點;
(2)求△ABC的面積.
(3)若△A1B1C1與△ABC關于x軸對稱,寫出A1、B1、C1的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 與
與![]() 在平面直角坐標系中的位置如圖所示.
在平面直角坐標系中的位置如圖所示.
(1)分別寫出各點的坐標:![]() ___________,
___________,![]() _________,
_________,![]() _______________.
_______________.
(2)![]() 是由
是由![]() 經過怎樣的平移變換得到的?答:___________________.
經過怎樣的平移變換得到的?答:___________________.
(3)若點![]() 是
是![]() 內部一點,則
內部一點,則![]() 內部的對應點
內部的對應點![]() 的坐標為___________.
的坐標為___________.
(4)求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究:
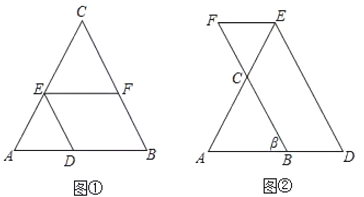
(1)如圖①,在![]() 中,點
中,點![]() 、
、![]() 、
、![]() 分別在邊
分別在邊![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的度數.請將下面的解答過程補充完整,并填空.
的度數.請將下面的解答過程補充完整,并填空.
(1)解:
![]() ,
,
![]() (兩直線平行,內錯角相等).
(兩直線平行,內錯角相等).
![]() ,
,
![]() (___________________________________).
(___________________________________).
![]() (__________________).
(__________________).
![]() .
.
應用:
(2)如圖②,在![]() 中,點
中,點![]() 、
、![]() 、
、![]() 分別在邊
分別在邊![]() 、
、![]() 、
、![]() 的延長線上,且
的延長線上,且![]() ,
,![]() ,若
,若,求
![]() 的大小.(用含
的大小.(用含![]() 的代數式表示).
的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“低碳環保,綠色出行”的概念得到廣大群眾的接受,越來越多的人喜歡選擇騎自行車作為出行工具.小軍和爸爸同時騎車去圖書館,爸爸先以150米/分的速度騎行一段時間,休息了5分鐘,再以m米/分的速度到達圖書館.小軍始終以同一速度騎行,兩人騎行的路程為y(米)與時間x(分鐘)的關系如圖.請結合圖象,解答下列問題:
(1)填空:a=________;b=________;m=________.
(2)若小軍的速度是 120 米/分,求小軍第二次與爸爸相遇時距圖書館的距離.
(3)在(2)的條件下,爸爸自第二次出發后,騎行一段時間后與小軍相距100 米,此時 小軍騎行的時間為________分鐘.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,動點P在平面直角坐標系中按圖中箭頭所示方向運動,第1次從原點運動到點(1,1),第2次接著運動到點(2,0),第3次接著運動到點(3,2),…,按這樣的運動規律,經過第2017次運動后,動點P的坐標是______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com