
【題目】端午節是中國的傳統節日.今年端午節前夕,遂寧市某食品廠抽樣調查了河東某居民區市民對A、B、C、D四種不同口味粽子樣品的喜愛情況,并將調查情況繪制成如圖兩幅不完整統計圖:
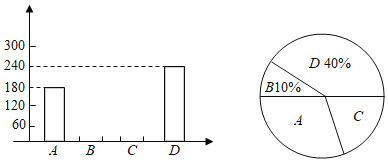
(1)本次參加抽樣調查的居民有 人.
(2)喜歡C種口味粽子的人數所占圓心角為 度.根據題中信息補全條形統計圖.
(3)若該居民小區有6000人,請你估計愛吃D種粽子的有 人.
(4)若有外型完全相同的A、B、C、D棕子各一個,煮熟后,小李吃了兩個,請用列表或畫樹狀圖的方法求他第二個吃的粽子恰好是A種粽子的概率.
【答案】(1)600;(2)72,圖見解析;(3)2400人;(4畫圖見解析,![]()
【解析】
(1)用喜歡D種口味粽子的人數除以它所占的百分比得到調查的總人數;
(2)先計算出喜歡B種口味粽子的人數,再計算出喜歡C種口味粽子的人數,則用360度乘以喜歡C種口味粽子的人數所占的百分比得到它在扇形統計圖中所占圓心角的度數,然后補全條形統計圖;
(3)用D占的百分比乘以6000即可得到結果;
(4)畫樹狀圖展示所有12種等可能的結果數,找出他第二個吃的粽子恰好是A種粽子的結果數,然后根據概率公式求解.
解:(1)240÷40%=600(人),
所以本次參加抽樣調查的居民有600人;
故答案為:600;
(2)喜歡B種口味粽子的人數為600×10%=60(人),
喜歡C種口味粽子的人數為600﹣180﹣60﹣240=120(人),
所以喜歡C種口味粽子的人數所占圓心角的度數為360°×![]() =72°;
=72°;
補全條形統計圖為:
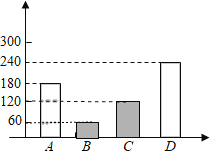
故答案為:72;
(3)6000×40%=2400,
所以估計愛吃D種粽子的有2400人;
故答案為2400;
(4)畫樹狀圖為:
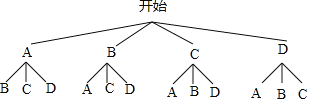
共有12種等可能的結果數,其中他第二個吃的粽子恰好是A種粽子的結果數為3,
所以他第二個吃的粽子恰好是A種粽子的概率=![]() =
=![]() .
.


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源: 題型:
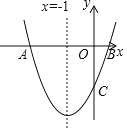
【題目】如圖,若二次函數y=ax2+bx+c(a≠0)圖象的對稱軸為x=1,與y軸交于點C,與x軸交于點A、點B(﹣1,0),則①二次函數的最大值為a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④當y>0時,﹣1<x<3,其中結論正確的有( )
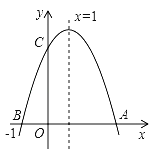
A.①③B.①④C.①②D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題背景)在面積都相等的所有矩形中,當其中一個矩形的一邊長為![]() 時,它的另一邊長為
時,它的另一邊長為![]() .求周長
.求周長![]() 的取值范圍.
的取值范圍.
(建立模型)
(1)設矩形相鄰兩邊的長分別為![]() ,
,![]() ,由題意可得
,由題意可得![]() ,則
,則![]() ,由周長為
,由周長為![]() ,得
,得![]() ,即
,即![]() ,滿足要求的
,滿足要求的![]() 的取值,從“圖形”角度考慮,應是函數
的取值,從“圖形”角度考慮,應是函數![]() 與 的圖象在第一象限內有公共點時
與 的圖象在第一象限內有公共點時![]() 的取值范圍;從“代數”角度考慮,應看作方程 有正數解時
的取值范圍;從“代數”角度考慮,應看作方程 有正數解時![]() 的取值范圍.
的取值范圍.
(畫圖觀察)
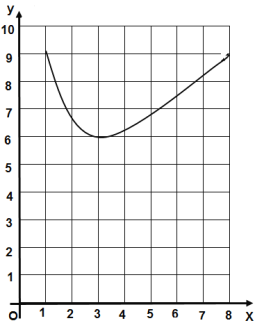
(2)函數![]() 的圖象如圖所示,而函數
的圖象如圖所示,而函數![]() 的圖象是一條與
的圖象是一條與![]() 軸平行的直線.當直線
軸平行的直線.當直線![]() 與函數
與函數![]() 的圖象有
的圖象有![]() 唯一公共點( , )時,周長
唯一公共點( , )時,周長![]() 取得最小值為 .
取得最小值為 .
(代數說理)
(3)圓圓說矩形的周長可以為![]() ,方方說矩形的周長可以為
,方方說矩形的周長可以為![]() ,你認為圓圓和方方的說法對嗎?為什么?
,你認為圓圓和方方的說法對嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2+bx+c與x軸交于A、B兩點,交y軸于點C,AB=4,對稱軸是直線x=﹣1.
(1)求拋物線的解析式及點C的坐標;
(2)連接AC,E是線段OC上一點,點E關于直線x=﹣1的對稱點F正好落在AC上,求點F的坐標;
(3)動點M從點O出發,以每秒2個單位長度的速度向點A運動,到達點A即停止運動,過點M作x軸的垂線交拋物線于點N,交線段AC于點Q.設運動時間為t(t>0)秒.
①連接BC,若△BOC與△AMN相似,請直接寫出t的值;
②△AOQ能否為等腰三角形?若能,求出t的值;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E是邊BC的中點,連接AE、DE,分別交BD、AC于點P、Q,過點P作PF⊥AE交CB的延長線于F,下列結論:
①∠AED+∠EAC+∠EDB=90°,
②AP=FP,
③AE=![]() AO,
AO,
④若四邊形OPEQ的面積為4,則該正方形ABCD的面積為36,
⑤CEEF=EQDE.
其中正確的結論有( )

A.5個B.4個C.3個D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是用黑色棋子擺成的美麗圖案,按照這樣的規律擺下去,第10個這樣的圖案需要黑色棋子的個數為( )

![]()


A.148B.152C.174D.202
查看答案和解析>>
科目:初中數學 來源: 題型:
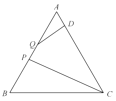
【題目】如圖,等邊![]() 的邊長為3,點
的邊長為3,點![]() 在邊
在邊![]() 上,
上,![]() ,線段
,線段![]() 在邊
在邊![]() 上運動,
上運動,![]() ,有下列結論:
,有下列結論:
①![]() 與
與![]() 可能相等;②
可能相等;②![]() 與
與![]() 可能相似;③四邊形
可能相似;③四邊形![]() 面積的最大值為
面積的最大值為![]() ;④四邊形
;④四邊形![]() 周長的最小值為
周長的最小值為![]() .其中,正確結論的序號為( )
.其中,正確結論的序號為( )
A.①④B.②④C.①③D.②③
查看答案和解析>>
科目:初中數學 來源: 題型:
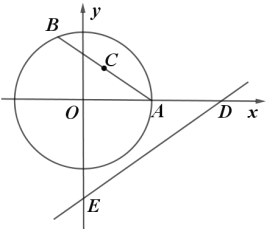
【題目】如圖,在平面直角坐標系![]() 中,半徑為2的
中,半徑為2的![]() 與
與![]() 軸的正半軸交于點
軸的正半軸交于點![]() ,點
,點![]() 是
是![]() 上一動點,點
上一動點,點![]() 為弦
為弦![]() 的中點,直線
的中點,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,則
,則![]() 面積的最小值為________.
面積的最小值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
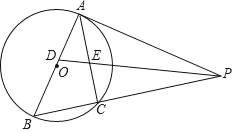
【題目】如圖,以AB為直徑的⊙O外接于△ABC,過A點的切線AP與BC的延長線交于點P,∠APB的平分線分別交AB,AC于點D,E,其中AE,BD(AE<BD)的長是一元二次方程x2﹣5x+6=0的兩個實數根.
(1)求證:PABD=PBAE;
(2)在線段BC上是否存在一點M,使得四邊形ADME是菱形?若存在,請給予證明,并求其面積;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com