

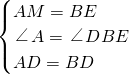 ,
, ,
, ,
,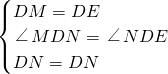 ,
,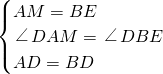 ,
,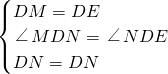 ,
,

 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
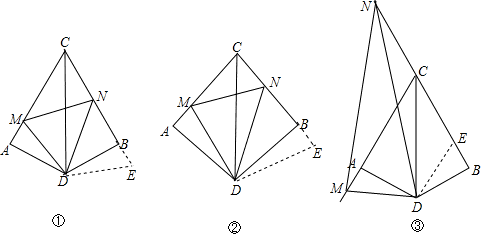
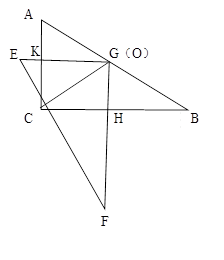
把兩個全等的直角三角板ABC和EFG疊放在一起,且使三角板EFG的直角頂點G與三角板ABC的斜邊中點O重合,其中∠B=∠F=30°,斜邊AB和EF的長均為4。
(1)當EG⊥AC于點K,GF⊥BC于點H時,如圖23-1,求GH:GK的值.
(2)現將三角板EFG由圖23-1所示的位置繞O點沿逆時針方向旋轉,旋轉角滿足條件:
0°<<30°,如圖23-2,EG交AC于點K,GF交BC于點H,GH:GK的值是否改變?證明你的結論.
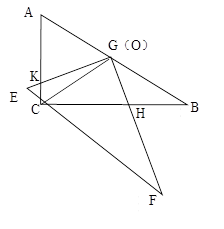
查看答案和解析>>
科目:初中數學 來源: 題型:
 角滿足條件:
角滿足條件: <30°,如圖23-2,EG交AC于點K,GF交BC于點H,GH:GK的值是否改變?證明你的結論.
<30°,如圖23-2,EG交AC于點K,GF交BC于點H,GH:GK的值是否改變?證明你的結論.

查看答案和解析>>
科目:初中數學 來源:2011屆湖南省岳陽市長煉中學初三上學期末數學卷 題型:解答題
把兩個全等的直角三角板ABC和EFG疊放在一起,且使三角板EFG的直角頂點G與三角板ABC的斜邊中點O重合,其中∠B=∠F=30°,斜邊AB和EF的長均為4。
(1)當EG⊥AC于點K,GF⊥BC于點H時,如圖23-1,求GH:GK的值.
(2)現將三角板EFG由圖23-1所示的位置繞O點沿逆時針方向旋轉,旋轉 角滿足條件:
角滿足條件:
0°< <30°,如圖23-2,EG交AC于點K,GF交BC于點H,GH:GK的值是否改變?證明你的結論.
<30°,如圖23-2,EG交AC于點K,GF交BC于點H,GH:GK的值是否改變?證明你的結論.

查看答案和解析>>
科目:初中數學 來源:2010-2011學年湖南省岳陽市初三上學期末數學卷 題型:解答題
把兩個全等的直角三角板ABC和EFG疊放在一起,且使三角板EFG的直角頂點G與三角板ABC的斜邊中點O重合,其中∠B=∠F=30°,斜邊AB和EF的長均為4。
(1)當EG⊥AC于點K,GF⊥BC于點H時,如圖23-1,求GH:GK的值.
(2)現將三角板EFG由圖23-1所示的位置繞O點沿逆時針方向旋轉,旋轉 角滿足條件:
角滿足條件:
0°< <30°,如圖23-2,EG交AC于點K,GF交BC于點H,GH:GK的值是否改變?證明你的結論.
<30°,如圖23-2,EG交AC于點K,GF交BC于點H,GH:GK的值是否改變?證明你的結論.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com