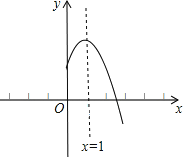
【題目】二次函數y＝ax2+bx+c（a，b，c是常數，a≠0）圖象的對稱軸是直線x＝1，其圖象的一部分如圖，對于下列說法：①abc＜0；②a﹣b+c＜0；③3a+c＜0；④當﹣1＜x＜3時，y＞0．其中正確的是（ ）
A.①②B.①③C.①②③D.①②④
【答案】C
【解析】
首先根據二次函數圖象開口方向可得a＜0，根據圖象與y軸交點可得c＞0，再根據二次函數的對稱軸x＝﹣
，結合a的取值可判定出b＞0，根據a、b、c的正負即可判斷出①的正誤；把x＝﹣1代入函數關系式y＝ax2+bx+c中得y＝a﹣b+c，再結合圖象判斷出②的正誤；把b＝﹣2a代入a﹣b+c中即可判斷出③的正誤；利用圖象可以直接看出④的正誤．
解：根據圖象可得：a＜0，c＞0，
對稱軸：x＝﹣＝1，
b＝﹣2a，
∵a＜0，
∴b＞0，
∴abc＜0，
故①正確；
把x＝﹣1代入函數關系式y＝ax2+bx+c中得：y＝a﹣b+c，
由圖象可以看出當x＝﹣1時，y＜0，
∴a﹣b+c＜0，
故②正確；
∵b＝﹣2a，
∴a﹣（﹣2a）+c＜0，
即：3a+c＜0，故③正確；
由圖形可以直接看出④錯誤．
正確的有①②③．
故選：C．
期末100分闖關海淀考王系列答案
小學能力測試卷系列答案科目：初中數學 來源： 題型：
【題目】某養豬場對豬舍進行噴藥消毒.在消毒的過程中，先經過
的藥物集中噴灑，再封閉豬舍
，然后再打開窗戶進行通風.已知室內每立方米空氣中含藥量
（
）與藥物在空氣中的持續時間
（
）之間的函數圖象如圖所示，其中在打開窗戶通風前與分別滿足兩個一次函數，在通風后與滿足反比例函數.
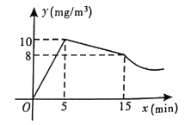
（1）求反比例函數的關系式；
（2）當豬舍內空氣中含藥量不低于
且持續時間不少于
，才能有效殺死病毒，問此次消毒是否有效？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“賞中華詩詞，尋文化基因，品生活之美”，某校舉辦了首屆“中國詩詞大會”，經選拔后有50名學生參加決賽，根據測試成績（成績都不低于50分）繪制出如圖所示的部分頻數分布直方圖．
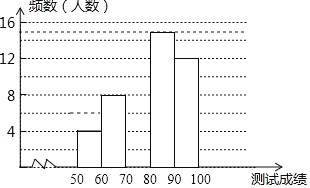
請根據圖中信息完成下列各題．
（1）將頻數分布直方圖補充完整人數；
（2）若測試成績不低于80分為優秀，則本次測試的優秀率是多少；
（3）現將從包括小明和小強在內的4名成績優異的同學中隨機選取兩名參加市級比賽，求小明與小強同時被選中的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點E是矩形ABCD對角線AC上的一個動點（點E可以與點A和點C重合），連接BE．已知AB=3cm，BC=4cm．設A、E兩點間的距離為xcm，BE的長度為ycm．
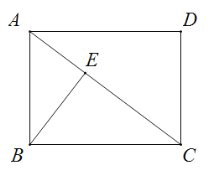
某同學根據學習函數的經驗，對函數y隨自變量x的變化而變化的規律進行探究．
下面是該同學的探究過程，請補充完整：
（1）通過取點、畫圖、測量及分析，得到了x與y的幾組值，如下表：
說明：補全表格時相關數值保留一位小數）
（2）建立平面直角坐標系，描出已補全后的表中各對對應值為坐標的點，畫出該函數的圖象．
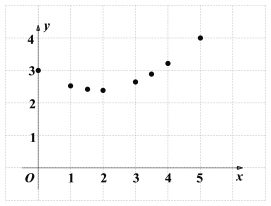
（3）結合畫出的函數圖象，解決問題：當BE=2AE時，AE的長度約為 cm．（結果保留一位小數）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某海濱浴場有100個遮陽傘，每個每天收費10元時，可全部租出，若每個每天提高2元，則減少10個傘租出，若每個每天收費再提高2元，則再減少10個傘租出，以此類推，為了投資少而獲利大，每個遮陽傘每天應提高_______________。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2019年9月，以“尋根國學，傳承文明”為主題的某市第三屆“國學少年強﹣﹣﹣國學知識挑戰賽”總決賽拉開帷幕．小明晉級了總決賽，比賽過程分兩個環節，參賽選手須在每個環節中各選擇一道題目．
第一環節：寫字注音、成語故事、國學常識、成語接龍（分別用A1，A2，A3，A4表示）；
第二環節：成語聽寫、詩詞對句、經典誦讀（分別用B1，B2，B3表示）．
（1）計算小明在第一環節抽取的題目是國學常識的概率；
（2）用樹狀圖或列表法，計算小明參加總決賽抽取題目都是成語題目（成語故事、成語接龍、成語聽寫）的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知正方形ABCD的頂點A、B在⊙O上，頂點C、D在⊙O內，將正方形ABCD繞點A逆時針旋轉，使點D落在⊙O上，若正方形ABCD的邊長和⊙O的半徑均為6cm，則點D運動的路徑長為（ ）
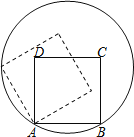
A.2πcmB.
cmC.πcmD.
cm
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，若點M是y軸正半軸上的任意一點，過點M作PQ∥x軸，分別交函數y＝
（y＞0）和y＝
（y＞0）的圖象于點P和Q，連接OP和OQ，則下列結論正確是（ ）
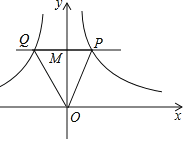
A.∠POQ不可能等于90°
B.
C.這兩個函數的圖象一定關于y軸對稱
D.△POQ的面積是
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AD是⊙O的切線，切點為A，AB是⊙O的弦，過點B作BC∥AD，交⊙O于點C，連接AC，過點C作CD∥AB，交AD于點D，連接AO并延長交BC于點M，交過點C的直線于點P，且∠BCP＝∠ACD．
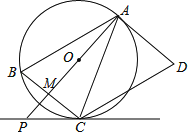
（1）求證：∠BAP＝∠CAP；
（2）判斷直線PC與⊙O的位置關系，并說明理由；
（3）若AB＝5
，BC＝10，求PC的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com