
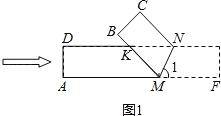
【題目】數學研究課上,老師帶領大家探究《折紙中的數學問題》時,出示如圖1所示的長方形紙條![]() ,其中
,其中![]() ,
,![]() .然后在紙條上任意畫一條截線段
.然后在紙條上任意畫一條截線段![]() ,將紙片沿
,將紙片沿![]() 折疊,
折疊,![]() 與
與![]() 交于點
交于點![]() ,得到
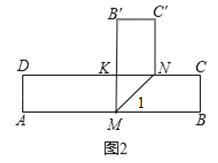
,得到![]() .如圖2所示:
.如圖2所示:

探究:
(1)若![]() ,
,![]() ______°;
______°;
(2)改變折痕![]() 位置,
位置,![]() 始終是______三角形,請說明理由;
始終是______三角形,請說明理由;
應用:
(3)愛動腦筋的小明在研究![]() 的面積時,發現
的面積時,發現![]() 邊上的高始終是個不變的值.根據這一發現,他很快研究出
邊上的高始終是個不變的值.根據這一發現,他很快研究出![]() 的面積最小值為
的面積最小值為![]() ,此時
,此時![]() 的大小可以為______°;
的大小可以為______°;
(4)小明繼續動手操作,發現了![]() 面積的最大值.請你求出這個最大值.
面積的最大值.請你求出這個最大值.
【答案】(1)![]() ;(2)等腰,證明詳見解析;(3)
;(2)等腰,證明詳見解析;(3)![]() 或
或![]() ;(4)
;(4)![]() 面積的最大值為
面積的最大值為![]()
【解析】
(1)根據矩形的性質和折疊的性質求出∠KNM,∠KMN的度數,根據三角形內角和即可求解;
(2)利用翻折變換的性質以及兩直線平行內錯角相等得出KM=KN;
(3)分兩種情況討論:①如圖2,利用當△KMN的面積最小值為![]() 時,KN=BC=1,故KN⊥B'M,得出∠1=∠NMB=45°;②如圖2(2),當△KMN的面積最小值為
時,KN=BC=1,故KN⊥B'M,得出∠1=∠NMB=45°;②如圖2(2),當△KMN的面積最小值為![]() 時,KN=KM=BC=1,故KM⊥B'M.由折疊的性質和周角的定義即可得出結論;
時,KN=KM=BC=1,故KM⊥B'M.由折疊的性質和周角的定義即可得出結論;
(4)分情況一:將矩形紙片對折,使點B與D重合,此時點K也與D重合;情況二:將矩形紙片沿對角線AC對折,此時折痕即為AC兩種情況討論求解.
(1)如圖1.
∵四邊形ABCD是矩形,∴AM∥DN,∴∠KNM=∠1.
∵∠1=70°,∴∠KNM=∠KMN=∠1=70°,∴∠MKN=40°.
故答案為:40;
(2)等腰.理由如下:
∵AB∥CD,∴∠1=∠MND.
∵將紙片沿MN折疊,∴∠1=∠KMN,∴∠MND=∠KMN,∴KM=KN.
故答案為:等腰;
(3)分兩種情況討論:①如圖2,當△KMN的面積最小值為![]() 時,KN=BC=1,故KN⊥B'M.
時,KN=BC=1,故KN⊥B'M.
∵∠NMB=∠KMN,∠KMB=90°,∴∠1=∠NMB=45°.
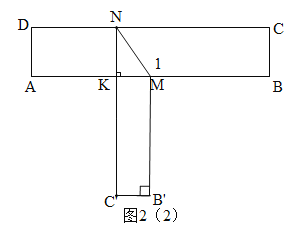
②如圖2(2),當△KMN的面積最小值為![]() 時,KN=KM=BC=1,故KM⊥B'M.
時,KN=KM=BC=1,故KM⊥B'M.
∵∠NMB=∠NMB',∠BMB'=90°,∴∠1=∠NMB=(360°-90°)÷2=135°.
故答案為:45°或135°;
(4)分兩種情況:
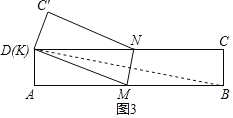
情況一:如圖3,將矩形紙片對折,使點B與D重合,此時點K也與D重合.
MK=MB=x,則AM=5﹣x.
由勾股定理得:12+(5﹣x)2=x2,
解得:x=2.6,∴MD=ND=2.6.
S△MNK=S△MND![]() 1×2.6=1.3.
1×2.6=1.3.
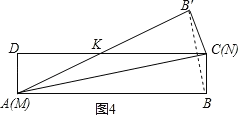
情況二:如圖4,將矩形紙片沿對角線AC對折,此時折痕即為AC.
MK=AK=CK=x,則DK=5﹣x.
同理可得:MK=NK=2.6.
∵MD=1,∴S△MNK![]() 1×2.6=1.3.
1×2.6=1.3.
△MNK的面積最大值為1.3.


科目:初中數學 來源: 題型:
【題目】模型建立:如圖1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直線
,直線![]() 經過點
經過點![]() ,過
,過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() .
.
(1)求證:![]() ;
;
(2)模型應用:
①已知直線l1:![]() 與y軸交于
與y軸交于![]() 點,將直線l1繞著
點,將直線l1繞著![]() 點順時針旋轉45°至l2,如圖2,求l2的函數解析式;
點順時針旋轉45°至l2,如圖2,求l2的函數解析式;
②如圖3,長方形ABCO,![]() 為坐標原點,
為坐標原點,![]() 的坐標為(8,6),
的坐標為(8,6),![]() 、
、![]() 分別在坐標軸上,
分別在坐標軸上,![]() 是線段
是線段![]() 上動點,點
上動點,點![]() 是直線
是直線![]() 上的一點,若△APD是以點D為直角頂點的等腰Rt△,請直接寫出點
上的一點,若△APD是以點D為直角頂點的等腰Rt△,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知x1、x2是關于x的﹣元二次方程(a﹣6)x2+2ax+a=0的兩個實數根.
(1)求a的取值范圍;
(2)若(x1+1)(x2+1)是負整數,求實數a的整數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ACB=∠ECD=90°,AC=BC,EC=DC,點D在AB邊上.

(1)求證:△ACE≌△BCD.
(2)若AE=3,AD=2.求ED的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(1,2),B(3,1),C(-2,-1).

(1)在圖中作出△ABC 關于 y 軸對稱的△A1B1C1并寫出坐標;
(2)求出△A1B1C1的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com