
【題目】經歷疫情復學后,學校開展了多種形式的防疫知識講座,并舉行了全員參加的“防疫”知識競賽,試卷題目共10題,每題10分.現分別從七年級1,2,3班中各隨機抽取10名同學的成績(單位:分).
收集整理數據如下:
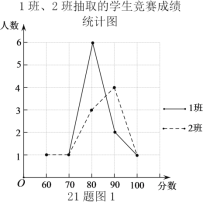
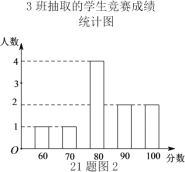
分析數據:
平均數 | 中位數 | 眾數 | |
1班 | 83 |
| 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根據以上信息回答下列問題:
(1)請直接寫出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比較這三組樣本數據的平均數、中位數和眾數,你認為哪個班的成績比較好?請說明理由(一條理由即可);
(3)為了讓學生重視安全知識的學習,學校將給競賽成績滿分的同學頒發獎狀,該校七年級學生共120人,試估計需要準備多少張獎狀?
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)我認為七年級2班的成績比較好,隨機抽取的樣本中,三個班樣本成績的平均數都為83, 2班成績的中位數為85,大于1班和3班成績的中位數80;2班成績的眾數90大于1班和3班成績的眾數80;(3)估計需要準備的獎狀是16張.
;(2)我認為七年級2班的成績比較好,隨機抽取的樣本中,三個班樣本成績的平均數都為83, 2班成績的中位數為85,大于1班和3班成績的中位數80;2班成績的眾數90大于1班和3班成績的眾數80;(3)估計需要準備的獎狀是16張.
【解析】
(1)根據平均數、眾數、中位數分別求解即可得到答案;
(2)根據三個班平均分都是83分,再分析中位數以及眾數,即可得到答案;
(3)根據調查人數的滿分情況估算總人數的滿分情況,即可得到答案;
解:(1)從條形統計圖得到:![]() ,
,
根據中位數的定義,1、2班調查人數為10人,即分數從小到大排序,第5第6名同學的平均成績即是中位數,
從折線圖得到1班70分一名同學,80分6名同學,
故![]() ,
,
從折線圖得到2班60分一名同學,70分一名同學,80分3名同學,90分四名同學,
故![]() ,
,
2班90分人數最多,故眾數c=90,
故:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)我認為七年級2班的成績比較好,理由如下:
隨機抽取的樣本中,三個班樣本成績的平均數都為83, 2班成績的中位數為85,大于1班和3班成績的中位數80;
2班成績的眾數90大于1班和3班成績的眾數80,
因此我認為2班成績較好 .
(3)因為所抽取的樣本中,樣本總量是30,而其中滿分人數是1+1+2=4.
所以,![]() .
.
答:估計需要準備的獎狀是16張.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案科目:初中數學 來源: 題型:
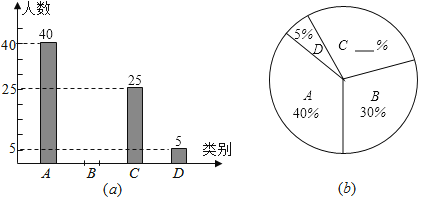
【題目】為了了解某區2018年初中畢業生畢業后的去向,某區教育部門對部分初三學生進行了抽樣調查,就初三學生的四種去向(A,讀普通高中;B,讀職業高中;C,直接進入社會就業;D,其它)進行數據統計,并繪制了兩幅不完整的統計圖(a)、(b).請問:
(1)此次共調查了多少名初中畢業生?
(2)將兩幅統計圖中不完整的部分補充完整;
(3)若某區2018年初三畢業生共有3500人,請估計2019年初三畢業生中讀普通高中的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
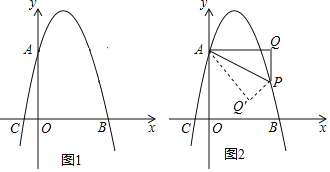
【題目】如圖1,已知拋物線y=﹣x2+bx+c交y軸于點A(0,4),交x軸于點B(4,0),點P是拋物線上一動點,試過點P作x軸的垂線1,再過點A作1的垂線,垂足為Q,連接AP.
(1)求拋物線的函數表達式和點C的坐標;
(2)若△AQP∽△AOC,求點P的橫坐標;
(3)如圖2,當點P位于拋物線的對稱軸的右側時,若將△APQ沿AP對折,點Q的對應點為點Q′,請直接寫出當點Q′落在坐標軸上時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,E是矩形ABCD的邊BC上一點,EF⊥AE,分別交AC,CD于點M,F,BG⊥AC,垂足為G,BG交AE于點H.
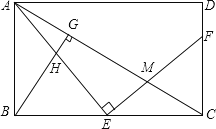
(1)求證:△ABE∽△ECF;
(2)找出與△ABH相似的三角形,并證明;
(3)若E是BC中點,BC=2AB,AB=4,求EM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知拋物線![]() 與x軸相交于A、B兩點(點A在點B的左側),與y軸交于點C.
與x軸相交于A、B兩點(點A在點B的左側),與y軸交于點C.
(1)求直線BC的解析式.
(2)點P是線段BC下方拋物線上的一個動點.
①求四邊形PBAC面積的最大值,并求四邊形PBAC面積的最大時P點的坐標;
②如果在x軸上存在點Q,使得以點B、C、P、Q為頂點的四邊形是平行四邊形.求點Q的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在正方形ABCD中,點E是邊BC上一點,連接AE,過點E作EM⊥AE,交對角線AC于點M,過點M作MN⊥AB,垂足為N,連接NE.


(1)求證:AE=![]() NE+ME;
NE+ME;
(2)如圖2,延長EM至點F,使EF=EA,連接AF,過點F作FH⊥DC,垂足為H.猜想CH與FH存在的數量關系,并證明你的結論;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,∠A=30°,將△ABC繞C點按逆時針方向旋轉![]() 角(0°<
角(0°<![]() <90°)得到△DEC,設CD交AB于點F,連接AD,當旋轉角
<90°)得到△DEC,設CD交AB于點F,連接AD,當旋轉角![]() 度數為________,△ADF是等腰三角形.
度數為________,△ADF是等腰三角形.
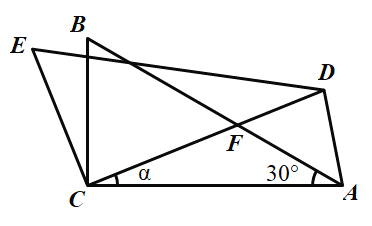
A.20°B.40°C.10°D.20°或40°
查看答案和解析>>
科目:初中數學 來源: 題型:
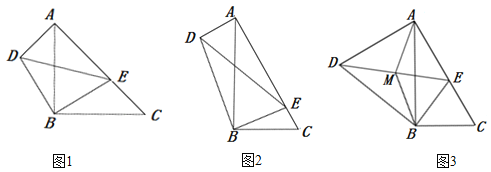
【題目】(1)問題發現
如圖1,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=45°,點E是線段AC上一動點,連接DE.
填空:①則![]() 的值為______;②∠EAD的度數為_______.
的值為______;②∠EAD的度數為_______.
(2)類比探究
如圖2,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=60°,點E是線段AC上一動點,連接DE.請求出![]() 的值及∠EAD的度數;
的值及∠EAD的度數;
(3)拓展延伸
如圖3,在(2)的條件下,取線段DE的中點M,連接AM、BM,若BC=4,則當△ABM是直角三角形時,求線段AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
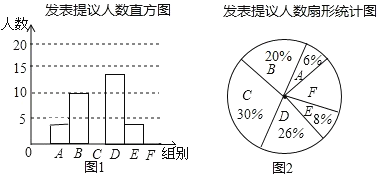
【題目】兩會期間,記者隨機抽取參會的部分代表,對他們某天發言的次數進行了統計,其結果如表,并繪制了如圖所示的兩幅不完整的統計圖,請結合圖中相關數據回答下列問題:
發言次數n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得樣本容量為 ,并補全直方圖;
(2)已知A組發表提議的代表中恰有1位女士,E組發表提議的代表中只有2位男士,現從A組與E組中分別抽一位代表寫報告,請用列表法或畫樹狀圖的方法,求所抽的兩位代表恰好都是男士的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com