
【題目】已知二次函數(shù)的圖象經(jīng)過點(diǎn)(2,3),頂點(diǎn)坐標(biāo)(1,4)
(1)求該二次函數(shù)的解析式;
(2)圖象與x軸的交點(diǎn)為A、B,與y軸的交點(diǎn)為C,求△ABC的面積.
【答案】(1)y=-(x-1)2+4;(2)S△ABC=6.
【解析】
(1)設(shè)出二次函數(shù)的頂點(diǎn)式y=a(x-1)2+4,將點(diǎn)(2,3)代入解析式,求出a的值即可得到函數(shù)解析式;
(2)令y=0,據(jù)此即可求出函數(shù)與x軸交點(diǎn)的橫坐標(biāo),從而得到圖象與x軸交點(diǎn)A、B兩點(diǎn)的坐標(biāo);由于知道C點(diǎn)坐標(biāo),根據(jù)A、B的坐標(biāo),求出AB的長,利用三角形的面積公式求出三角形的面積.
(1)設(shè)所求的二次函數(shù)的解析式為y= a(x-1)2+4,
把x=2,y=3代入上式,得:
3=a(2-1)2+4,
解得:a=1,
∴所求的二次函數(shù)解析式為y=(x-1)2+4,
即y=x2+2x+3.
(2)當(dāng)y=0時(shí),0= x2+2x+3,
解得:![]() =1,
=1,![]() =3,
=3,
∴圖象與x軸交點(diǎn)A. B兩點(diǎn)的坐標(biāo)分別為(1,0),(3,0),
由題意得:C點(diǎn)坐標(biāo)為(0,3),AB=4,
∴S△ABC= ![]() ×4×3=6.
×4×3=6.


 新思維假期作業(yè)暑假吉林大學(xué)出版社系列答案
新思維假期作業(yè)暑假吉林大學(xué)出版社系列答案 藍(lán)天教育暑假優(yōu)化學(xué)習(xí)系列答案
藍(lán)天教育暑假優(yōu)化學(xué)習(xí)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知點(diǎn) ![]() 是線段
是線段 ![]() 上一點(diǎn),
上一點(diǎn),![]() ,
,![]() ,
,![]() .
.
(1)線段 ![]() 繞點(diǎn) 逆時(shí)針旋轉(zhuǎn) °可與線段
繞點(diǎn) 逆時(shí)針旋轉(zhuǎn) °可與線段 ![]() 重合.
重合.
(2)若 ![]() ,則
,則 ![]() °.
°.
(3)若 ![]() ,
,![]() ,則
,則 ![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我們知道,在平面內(nèi),如果一個(gè)圖形繞著一個(gè)定點(diǎn)旋轉(zhuǎn)一定的角度后能與自身重合,那么就稱這個(gè)圖形是旋轉(zhuǎn)對稱圖形,轉(zhuǎn)的這個(gè)角稱為這個(gè)圖形的一個(gè)旋轉(zhuǎn)角.例如,正方形繞著它的對角線的交點(diǎn)旋轉(zhuǎn)![]() 后能與自身重合所以正方形是旋轉(zhuǎn)對稱圖形,它有一個(gè)旋轉(zhuǎn)角為
后能與自身重合所以正方形是旋轉(zhuǎn)對稱圖形,它有一個(gè)旋轉(zhuǎn)角為![]() .
.

![]() 判斷下列說法是否正確(在相應(yīng)橫線里填上“對”或“錯(cuò)”)
判斷下列說法是否正確(在相應(yīng)橫線里填上“對”或“錯(cuò)”)
①正五邊形是旋轉(zhuǎn)對稱圖形,它有一個(gè)旋轉(zhuǎn)角為![]() .________
.________
②長方形是旋轉(zhuǎn)對稱圖形,它有一個(gè)旋轉(zhuǎn)角為![]() .________
.________
![]() 填空:下列圖形中時(shí)旋轉(zhuǎn)對稱圖形,且有一個(gè)旋轉(zhuǎn)角為
填空:下列圖形中時(shí)旋轉(zhuǎn)對稱圖形,且有一個(gè)旋轉(zhuǎn)角為![]() 的是________.(寫出所有正確結(jié)論的序號(hào))
的是________.(寫出所有正確結(jié)論的序號(hào))
①正三角形②正方形③正六邊形④正八邊形
![]() 寫出兩個(gè)多邊形,它們都是旋轉(zhuǎn)對稱圖形,都有一個(gè)旋轉(zhuǎn)角為
寫出兩個(gè)多邊形,它們都是旋轉(zhuǎn)對稱圖形,都有一個(gè)旋轉(zhuǎn)角為![]() ,其中一個(gè)是軸對稱圖形,但不是中心對稱圖形;另一個(gè)既是軸對稱圖形,又是中心對稱圖形.
,其中一個(gè)是軸對稱圖形,但不是中心對稱圖形;另一個(gè)既是軸對稱圖形,又是中心對稱圖形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)y=ax2+bx+c(a≠0)的部分圖象如圖所示,圖象過點(diǎn)(﹣1,0),對稱軸為直線x=2,下列結(jié)論:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若點(diǎn)A(﹣3,y1)、點(diǎn)B(﹣![]() ,y2)、點(diǎn)C(
,y2)、點(diǎn)C(![]() ,y3)在該函數(shù)圖象上,則y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2,且x1<x2,則x1<﹣1<5<x2.其中正確的結(jié)論有( )
,y3)在該函數(shù)圖象上,則y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2,且x1<x2,則x1<﹣1<5<x2.其中正確的結(jié)論有( )

A. 2個(gè) B. 3個(gè) C. 4個(gè) D. 5個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
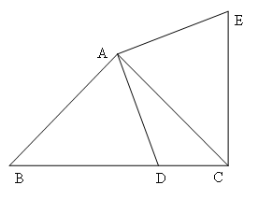
【題目】如圖,在△ABC中,∠B=60°,AD平分∠BAC,CE平分∠BCA,AD、CE交于點(diǎn)F,CD=CG,連結(jié)FG.

(1)求證:FD=FG;
(2)線段FG與FE之間有怎樣的數(shù)量關(guān)系,請說明理由;
(3)若∠B≠60°,其他條件不變,則(1)和(2)中的結(jié)論是否仍然成立?請直接寫出判斷結(jié)果,不必說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有兩個(gè)內(nèi)角分別是它們對角的一半的四邊形叫做半對角四邊形
(1)如圖1,在半對角四邊形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A,求∠B與∠C的度數(shù)之和;
∠A,求∠B與∠C的度數(shù)之和;
(2)如圖2,銳角△ABC內(nèi)接于⊙O,若邊AB上存在一點(diǎn)D,使得BD=BO,∠OBA的平分線交OA于點(diǎn)E,連結(jié)DE并延長交AC于點(diǎn)F,∠AFE=2∠EAF.求證:四邊形DBCF是半對角四邊形;
(3)如圖3,在(2)的條件下,過點(diǎn)D作DG⊥OB于點(diǎn)H,交BC于點(diǎn)G,當(dāng)DH=BG=2時(shí),求⊙O的直徑.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某歌星演唱會(huì)票價(jià)如下:甲種票每張200元,乙種票每張100元.工會(huì)小組準(zhǔn)備了1000元,全部用來買票,且每種至少買一張.
(1)共有多少種購票方案?列舉出所有可能結(jié)果;
(2)如果從上述方案中任意選中一種方案購票,求恰好買到7張門票的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】鹽阜人民商場經(jīng)營某種品牌的服裝,購進(jìn)時(shí)的單價(jià)是![]() 元,根據(jù)市場調(diào)查:在一段時(shí)間內(nèi),銷售單價(jià)是
元,根據(jù)市場調(diào)查:在一段時(shí)間內(nèi),銷售單價(jià)是![]() 元時(shí),銷售量是
元時(shí),銷售量是![]() 件,而銷售單價(jià)每漲
件,而銷售單價(jià)每漲![]() 元,就會(huì)少售出
元,就會(huì)少售出![]() 件服裝.
件服裝.
![]() 設(shè)該種品牌服裝的銷售單價(jià)為
設(shè)該種品牌服裝的銷售單價(jià)為![]() 元
元![]() ,銷售量為
,銷售量為![]() 件,請寫出
件,請寫出![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
![]() 若商場獲得了
若商場獲得了![]() 元銷售利潤,該服裝銷售單價(jià)
元銷售利潤,該服裝銷售單價(jià)![]() 應(yīng)定為多少元?
應(yīng)定為多少元?
![]() 在
在![]() 問條件下,若該商場要完成不少于
問條件下,若該商場要完成不少于![]() 件的銷售任務(wù),求商場銷售該品牌服裝獲得的最大利潤是多少?
件的銷售任務(wù),求商場銷售該品牌服裝獲得的最大利潤是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
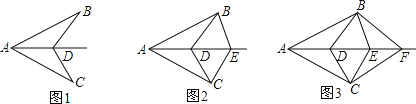
【題目】已知AB=AC,AD為∠BAC的角平分線,D、E、F…為∠BAC的角平分線上的若干點(diǎn).如圖1,連接BD、CD,圖中有1對全等三角形;如圖2,連接BD、CD、BE、CE,圖中有3對全等三角形;如圖3,連接BD、CD、BE、CE、BF、CF,圖中有6對全等三角形;依此規(guī)律,第n個(gè)圖形中有_____對全等三角形.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com