
【題目】已知∠α的頂點在正n邊形的中心點O處,∠α繞著頂點O旋轉,角的兩邊與正n邊 形的兩邊分別交于點M、N,∠α與正n邊形重疊部分面積為S.
(1)當n=4,邊長為2,∠α=90°時,如圖(1),請直接寫出S的值;
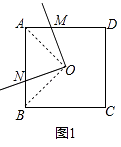
(2)當n=5,∠α=72°時,如圖(2),請問在旋轉過程中,S是否發生變化?并說明理由;
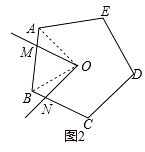
(3)當n=6,∠α=120°時,如圖(3),請猜想S是原正六邊形面積的幾分之幾(不必說明理由).若∠α的平分線與BC邊交于點P,判斷四邊形OMPN的形狀,并說明理由.
【答案】
(1)
解:如圖1,連接OA、OB,
當n=4時,四邊形ABCD是正方形,
∴OA=OB,AO⊥BO,
∴∠AOB=90°,
∴∠AON+∠BON=90°,
∵∠MON=∠α=90°,
∴∠AON+∠AOM=90°,
∴∠BON=∠AOM,
∵O是正方形ABCD的中心,
∴∠OAM=∠ABO=45°,
在△AOM和△BON中,
∵ 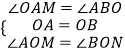 ,
,
∴△AOM≌△BON(ASA),
∴S△AOM=S△BON,
∴S△AOM+S△AON=S△BON+S△AON,
即S四邊形ANDM=S△ABO=S,
∵正方形ABCD的邊長為2,
∴S正方形ABCD=2×2=4,
∴S=S△ABO= ![]() S正方形ABCD=
S正方形ABCD= ![]() ×4=1
×4=1
(2)
解:如圖2,在旋轉過程中,∠α與正n邊形重疊部分的面積S不變,
理由如下:連接OA、OB,
則OA=OB=OC,∠AOB=∠MON=72°,
∴∠AOM=∠BON,且∠OAB=∠OBC=54°,
∴△OAM≌△OBN,
∴四邊形OMBN的面積:S=S△OBN+S△OBM=S△OAM+S△OBM=S△OAB,
故S的大小不變
(3)
解:猜想:S是原正六邊形面積的 ![]() ,理由是:
,理由是:
如圖3,連接OB、OD,
同理得△BOM≌△DON,
∴S=S△BOM+S四邊形OBCN=S△DON+S四邊形OBCN=S四邊形OBCD= ![]() S六邊形ABCDEF;
S六邊形ABCDEF;
四邊形OMPN是菱形,
理由如下:
如圖4,作∠α的平分線與BC邊交于點P,
連接OA、OB、OC、OD、PM、PN,
∵OA=OB=OC=OD,∠AOB=∠BOC=∠COD=∠MOP=∠PON=60°,
∴∠OAM=∠OBP=∠OCN=60°,∠AOM=∠BOP=∠CON,
∴△OAM≌△OBP≌△OCN,
∴OM=OP=ON,
∴△OMP和△OPN都是等邊三角形,
∴OM=PM=OP=ON=PN,
∴四邊形OMPN是菱形.

【解析】(1)如圖1,連接對角線OA、OB,證明△AOM≌△BON(ASA),則S△AOM=S△BON , 所以S=S△ABO= ![]() S正方形ABCD=
S正方形ABCD= ![]() ×4=1;(2)如圖2,在旋轉過程中,∠α與正n邊形重疊部分的面積S不變,連接OA、OB,同理證明△OAM≌△OBN,則S=S△OBN+S△OBM=S△OAM+S△OBM=S△OAB , 故S的大小不變;(3)如圖3,120°相當于兩個中心角,可以理解為一個中心角連續旋轉兩次,由前兩問的推理得,旋轉一個中心角時重疊部分的面積是原來正n邊形面積的
×4=1;(2)如圖2,在旋轉過程中,∠α與正n邊形重疊部分的面積S不變,連接OA、OB,同理證明△OAM≌△OBN,則S=S△OBN+S△OBM=S△OAM+S△OBM=S△OAB , 故S的大小不變;(3)如圖3,120°相當于兩個中心角,可以理解為一個中心角連續旋轉兩次,由前兩問的推理得,旋轉一個中心角時重疊部分的面積是原來正n邊形面積的 ![]() ,則S是原正六邊形面積的
,則S是原正六邊形面積的 ![]() ;也可以類比(1)(2)證明△OAM≌△OBN,利用割補法求出結論;
;也可以類比(1)(2)證明△OAM≌△OBN,利用割補法求出結論;
四邊形OMPN是菱形,
理由如下:如圖4,作∠α的平分線與BC邊交于點P,作輔助線構建全等三角形,同理證明△OAM≌△OBP≌△OCN,得△OMP和△OPN都是等邊三角形,則OM=PM=OP=ON=PN,根據四邊相等的四邊是菱形可得:四邊形OMPN是菱形.
【考點精析】解答此題的關鍵在于理解旋轉的性質的相關知識,掌握①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:
【題目】黔東南州某校吳老師組織九(1)班同學開展數學活動,帶領同學們測量學校附近一電線桿的高.已知電線桿直立于地面上,某天在太陽光的照射下,電線桿的影子(折線BCD)恰好落在水平地面和斜坡上,在D處測得電線桿頂端A的仰角為30°,在C處測得電線桿頂端A得仰角為45°,斜坡與地面成60°角,CD=4m,請你根據這些數據求電線桿的高(AB).
(結果精確到1m,參考數據: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點O為直線AB上一點,過點O作射線OC,使∠BOC=120°,將一直角三角板的直角頂點放在點O處,一邊OM在射線OB上,另一邊ON在直線AB的下方.
(1)將圖1中的三角板繞點O逆時針旋轉至圖2,使一邊OM在∠BOC的內部,且恰好平分∠BOC,設ON的反向延長線為OD,則∠COD= °,∠AOD= °.
(2)將圖1中的三角板繞點O順時針旋轉至圖3,使ON在∠AOC的內部,求∠AOM﹣∠NOC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進一種單價為40元的書包,如果以單價50元出售,那么每月可售出30個,根據銷售經驗,售價每提高5元,銷售量相應減少1個.
(1)請寫出銷售單價提高x元與總的銷售利潤y元之間的函數關系式;
(2)如果你是經理,為使每月的銷售利潤最大,那么你確定這種書包的單價為多少元?此時,最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形網格中,△AOB的頂點均在格點上,點A、B的坐標分別是A(3,2)、B(1,3).將△AOB繞點O逆時針旋轉90°后得到△A1OB1 . 
(1)畫出旋轉后的△A1OB1 , 點A1的坐標為;
(2)在旋轉過程中,點B經過的路徑為 ![]() ,求
,求 ![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:二次函數y=ax2+bx+c的圖像所示,下列結論中:①abc>0;②2a+b=0;③當m≠1時,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 則x1+x2=2,正確的個數為( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人進行摸牌游戲.現有三張形狀大小完全相同的牌,正面分別標有數字2,3,5.將三張牌背面朝上,洗勻后放在桌子上.甲從中隨機抽取一張牌,記錄數字后放回洗勻,乙再隨機抽取一張.
(1)請用列表法或畫樹狀圖的方法,求兩人抽取相同數字的概率;
(2)若兩人抽取的數字和為2的倍數,則甲獲勝;若抽取的數字和為5的倍數,則乙獲勝.這個游戲公平嗎?請用概率的知識加以解釋.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com