
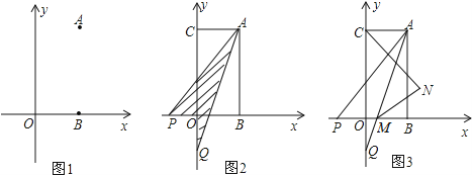
【題目】如圖:已知在平面直角坐標系中點A(a,b)點B(a,0),且滿足|2a-b|+(b-4)2=0.
(1)求點A、點B的坐標;
(2)已知點C(0,b),點P從B點出發(fā)沿x軸負方向以1個單位每秒的速度移動.同時點Q從C點出發(fā),沿y軸負方向以2個單位每秒的速度移動,某一時刻,如圖所示且S陰=![]() S四邊形OCAB,求點P移動的時間;
S四邊形OCAB,求點P移動的時間;
(3)在(2)的條件下,AQ交x軸于M,作∠ACO,∠AMB的角平分線交于點N,判斷![]() 是否
是否![]() 為定值,若是定值求其值;若不是定值,說明理由.
為定值,若是定值求其值;若不是定值,說明理由.
【答案】(1)點A(2,4)、點B(2,0);(2)3s;(3)是定值,![]()
【解析】
(1)根據(jù)非負數(shù)的性質(zhì)易得a=2,b=4,則點A的坐標為(2,4)、點B的坐標(2,0);
(2)設P點運動時間為t,則t>2,則P點坐標可表示為(2-t,0),Q點坐標表示為(0,4-2t),用待定系數(shù)法確定直線AQ的解析式為y=tx+4-2t,則可確定直線AQ與x軸交點坐標為(![]() ,0),根據(jù)題意得
,0),根據(jù)題意得![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4)=
×(2t-4)=![]() ×2×4,然后解方程求出t的值;
×2×4,然后解方程求出t的值;
(3)先根據(jù)角平分線定義得∠ACN=45°,∠1=∠2,再由AC∥BP得∠CAM=∠AMB=2∠1,然后根據(jù)三角形內(nèi)角和定理得∠ACN+∠CAM=∠N+∠1,所以∠N=45°+∠1,再根據(jù)三角形外角性質(zhì)得∠AMB=∠APB+∠PAQ,即∠APB+∠PAQ=2∠1,接著根據(jù)三角形內(nèi)角和定理得∠AQC+∠OMQ=90°,利用∠OMQ=2∠1可得∠AQC=90°-2∠1,最后用∠1表示式子![]() 中的角,約分即可得到
中的角,約分即可得到![]() =
=![]() .
.
解:(1)∵|2a-b|+(b-4)2=0.
∴2a-b=0,b-4=0,
∴a=2,b=4,
∴點A的坐標為(2,4)、點B的坐標(2,0);
(2)如圖2,設P點運動時間為t,則t>2,所以P點坐標為(2-t,0),Q點坐標為(0,4-2t),
設直線AQ的解析式為y=kx+4-2t,
把A(2,4)代入得2k+4-2t=4,解得k=t,
∴直線AQ的解析式為y=tx+4-2t,
直線AQ與x軸交點坐標為(![]() ,0),
,0),
∴S陰影=![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4),
×(2t-4),
而S陰=![]() S四邊形OCAB,
S四邊形OCAB,
∴![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4)=
×(2t-4)=![]() ×2×4,
×2×4,
整理得t2-3t=0,
解得t1=0(舍去),t2=3,
∴點P移動的時間為3s;
(3)![]() 為定值.理由如下:
為定值.理由如下:
如圖3,∵∠ACO,∠AMB的角平分線交于點N,
∴∠ACN=45°,∠1=∠2,
∵AC∥BP,
∴∠CAM=∠AMB=2∠1,
∵∠ACN+∠CAM=∠N+∠1,
∴45°+2∠1=∠N+∠1,
∴∠N=45°+∠1,
∵∠AMB=∠APB+∠PAQ,
∴∠APB+∠PAQ=2∠1,
∵∠AQC+∠OMQ=90°,
而∠OMQ=2∠1,
∴∠AQC=90°-2∠1,
∴![]() =
=![]() =
=![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】如圖1,O為直線AB上一點,過點O作射線OC,![]() ,將一直角三角板
,將一直角三角板![]() 的直角頂點放在點O處,一邊ON在射線OA上,另一邊OM與OC都在直線AB的上方.
的直角頂點放在點O處,一邊ON在射線OA上,另一邊OM與OC都在直線AB的上方.
![]() 將圖1中的三角板繞點O以每秒
將圖1中的三角板繞點O以每秒![]() 的速度沿逆時針方向旋轉(zhuǎn)一周
的速度沿逆時針方向旋轉(zhuǎn)一周![]() 如圖2,經(jīng)過t秒后,ON落在OC邊上,則
如圖2,經(jīng)過t秒后,ON落在OC邊上,則![]() ______秒
______秒![]() 直接寫結果
直接寫結果![]() .
.
![]() 如圖2,三角板繼續(xù)繞點O以每秒
如圖2,三角板繼續(xù)繞點O以每秒![]() 的速度沿逆時針方向旋轉(zhuǎn)到起點OA上
的速度沿逆時針方向旋轉(zhuǎn)到起點OA上![]() 同時射線OC也繞O點以每秒
同時射線OC也繞O點以每秒![]() 的速度沿逆時針方向旋轉(zhuǎn)一周,
的速度沿逆時針方向旋轉(zhuǎn)一周,
![]() 當OC轉(zhuǎn)動9秒時,求
當OC轉(zhuǎn)動9秒時,求![]() 的度數(shù).
的度數(shù).
![]() 運動多少秒時,
運動多少秒時,![]() ?請說明理由.
?請說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知∠BAC的平分線與BC的垂直平分線PQ相交于點P,PM⊥AC,PN⊥AB,垂足分別為M、N,AB=5,AC=11,則CM的長度為( )
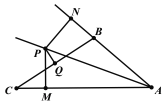
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在正方形方格中,陰影部分是涂黑3個小正方形所形成的圖案.
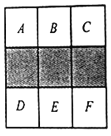
(1)如果將一粒米隨機地拋在這個正方形方格上,那么米粒落在陰影部分的概率是多少?
(2)現(xiàn)將方格內(nèi)空白的小正方形(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )中任取2個涂黑,得到新圖案.請用列表或畫樹狀圖的方法求新圖案是軸對稱圖形的概率.
)中任取2個涂黑,得到新圖案.請用列表或畫樹狀圖的方法求新圖案是軸對稱圖形的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
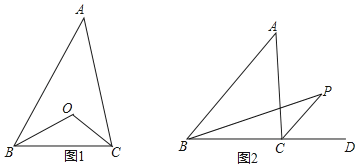
【題目】(1)如圖1,△ABC中,BO平分∠ABC,CO平分∠ACB,∠A=56°,求∠BOC的度數(shù);
(2)如圖2,若點P為△ABC外部一點,PB平分∠ABC,PC平分外角∠ACD,先寫出∠A和∠P的數(shù)量關系,并證明你的結論.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直線AB是某天然氣公司的主輸氣管道,點C、D是在AB異側(cè)的兩個小區(qū),現(xiàn)在主輸氣管道上尋找支管道連接點,向兩個小區(qū)鋪設管道![]() 有以下兩個方案:
有以下兩個方案:
方案一:只取一個連接點P,使得像兩個小區(qū)鋪設的支管道總長度最短,在圖中標出點P的位置,保留畫圖痕跡;
方案二:取兩個連接點M和N,使得點M到C小區(qū)鋪設的支管道最短,使得點N到D小區(qū)鋪設的管道最![]() 短在途中標出M、N的位置,保留畫圖痕跡;
短在途中標出M、N的位置,保留畫圖痕跡;

設方案一中鋪設的支管道總長度為L1![]() ,方案二中鋪設的支管道總長度為
,方案二中鋪設的支管道總長度為![]() ,則L1與L2的大小關系為: L1_____ L2(填
,則L1與L2的大小關系為: L1_____ L2(填![]() ”、
”、![]() ”或)理由是______.
”或)理由是______.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了深入踐行素質(zhì)教育,落實學生的核心素養(yǎng),培養(yǎng)全面發(fā)展的人,育紅中學積極開展校本課程建設,促進學生的個性發(fā)展,計劃成立“![]() .陶藝社團、
.陶藝社團、![]() .航模社團、
.航模社團、![]() .足球社團、
.足球社團、![]() .
.![]() 科技社團、
科技社團、![]() .其他”,規(guī)定每位學生選報一個.為了了解報名情況,隨機抽取了部分學生進行調(diào)查,將所有調(diào)查結果整理后繪制成不完整的條形統(tǒng)計圖(如圖1)和扇形統(tǒng)計圖(如圖2),請結合統(tǒng)計圖回答下列問題:
.其他”,規(guī)定每位學生選報一個.為了了解報名情況,隨機抽取了部分學生進行調(diào)查,將所有調(diào)查結果整理后繪制成不完整的條形統(tǒng)計圖(如圖1)和扇形統(tǒng)計圖(如圖2),請結合統(tǒng)計圖回答下列問題:
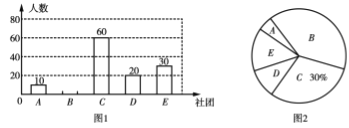
(1)在這次調(diào)查中,一共調(diào)查了_______名學生;
(2)扇形統(tǒng)計圖中,扇形![]() 的圓心角度數(shù)是_______;
的圓心角度數(shù)是_______;
(3)請補全條形統(tǒng)計圖;
(4)若該校共有6800名學生,請估計全校選擇“![]() 科技社團”的學生人數(shù).
科技社團”的學生人數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】甲、乙兩人準備在一段長為1200米的筆直公路上進行跑步,甲、乙跑步的速度分別為4m/s和6m/s,起跑前乙在起點,甲在乙前面100米處,若同時起跑,則兩人從起跑至其中一人先到達終點的過程中,甲、乙兩之間的距離y(m)與時間t(s)的函數(shù)圖象是( )
A. 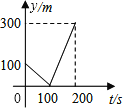 B.
B. 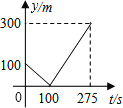
C. 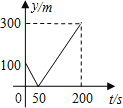 D.
D. 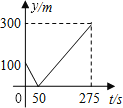
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com